تعریف آمار: روش علمی است که برای جمع آوری، تلخیص، تجزیه و تحلیل، تفسیر و بطور کلی برای مطالعه و بررسی مشاهدات بکار گرفته میشود.
استفاده از فنون آماری برای مقاصد ذیل:
1- برای تبدیل دادهها به اطلاعات (با بررسی قیمت سهام در مورد آینده قیمت آنها نظر دادن)
2- برای بررسی صحت و سقم فرضیات (اجرای یک سیستم اتوماسیون نامه نگاری در سرعت رسیدگی به مراجعات تاثیری دارد یا نه؟)
3- برای تعیین اعتبار و پایایی تحقیقات پرسشنامهای و مصاحبهای ( پرسشنامه GHQ در بررسی سلامت روانی افراد به خوبی عمل میکند. پرسشنامه GHQ-28 یک ابزار سنجش است که برای ارزیابی وضعیت روانی فرد به کار میرود. GHQ مخفف عبارت General Health Questionnaire است و شامل 28 سوال درباره علائم روانی است که شامل مسائلی مانند اضطراب، افسردگی، خودکشی، ناراحتی، خستگی، بیخوابی و … میشود.)
جامعه: جامعه بزرگترین مجموعه از موجودات است که در یک زمان معین، مطلوب قرار میگیرند. مثل جامعه فرهنگیان ایران و . . .
لازم به ذکر است جامعه متناسب با هدف تغییر میکند. به طور مثال اگر هدف بررسی رضایتمندی کارکنان بانک مرکزی باشد، جامعه مورد نظر تمام کارکنان بانک مرکزی است.
اگر هدف بررسی رضایتمندی معلمان باشد جامعه به صورت تمام معلمان تعریف میشود و..
جامعه آماری: تعدادی از عناصر مطلوب مورد نظر که حداقل دارای یک صفت مشخصه باشند.
- صفت مشخصه: صفتی است که بین همه عناصر جامعه آماری مشترک و متمایز کننده جامعه آماری از سایر جوامع باشد.
انواع جامعه آماری
1- محدود : یعنی جامـعه مقادیر از تعـداد محدود و ثابتی تشکیل شده و پایان پذیر باشد. (کارکنان بانک مرکزی)
2- نامحدود : یعنی جامعه از یک ردیف بیانتهایی از مقادیر تشکیل شده باشد. ( تمام برگهای درختان)
- تعریف نمونه: نمونه عبارتست از تعداد محدودی از آحاد جامعه آماری که بیان کننده ویژگیهای اصلی جامعه باشد. ( نمونه انتخاب شده باشد تا حد ممکن شبیه جامعه مورد نظر باشد. برای بررسی یک روش آموزش درست نیست فقط دانشجویان با معدل بالا را انتخاب کرد بلکه انتخاب دانشجویان از هر طیف معدل الزامی است.)
انواع شاخصهای آماری
1- پارامتر : شاخـصهایی که از طریق سرشـماری ( انـدازه گیری تمامی عناصـر جامعه آماری ) بدست میآیند. ( محاسبه متوسط درآمد کارکنان بانک مرکزی با استفاده از اندازه گیری درآمد تمام کارکنان دولت.)
2- آماره : شاخـصهایی که از طریق نمـونه گیری ( اندازه گیری بخشی از جامعه ) بدست میآیند. ( محاسبه متوسط درآمد کارکنان بانک مرکزی با استفاده از اندازه گیری درآمد نمونهای از کارکنان دولت.)
روشهای ناپارامتریک
در جوامع آماری که از توزیع نرمال برخوردار نیستند و دادههای غیرکمی (کیفی) با نمونههای کوچک را میتوان با این فنون بررسی کرد.
سیر تحول علم آمار از نظر موضوعی عبارت است از:
• آمار توصیفی: این نوع آمار به توصیف جامعه میپردازد و هدف آن محاسبه پارامترهای جامعه است. چنانچه محاسبه مقادیر و شاخصهای جامعه آماری با استفاده از سرشماری تمامی عناصر آن انجام گیرد به آن آمار توصیفی گویند.
• آمار استنباطی: در این نوع آمار با استفاده از مقادیر نمونه، آمارهها محاسبه شده و به کمک تخمین و آزمون فرض آماری، آمارهها به پارامترهای جامعه تعمیم داده میشود. ( در بحثهای آماری هرجا سخن از استنباط و استنتاج باشد، به آن آمار استنباطی گویند.)
• آمار ناپارامتریک: آمار ناپارامتریک در مقابل آمار پارامتریک مطرح میشود یکی از فرضهای اساسی در آمار پارامتریک برخوردار بودن مشاهدات از تویع نرمال است، در حالی که در فنون ناپارامتریک این فرض ضرورتی ندارد. در بررسیهایی که متغیرهای آنها دارای مقیاس کیفی هستند، از این روشها استفاده میشود چرا که متغیرهایی که دارای مقیاس کیفی هستند فاقد توزیع آماری بوده و به آنها آزاد توزیع گویند.
مراحل پژوهش علمی در آمار
1- مشخص کردن هدف
2- جمع آوری دادهها
3- تجزیه و تحلیل دادهها
4- بیان یافتهها
دو عنصر اصلی تحقیقات رفتاری و مدیریتی
1- فرضیههای تحقیق
2- متغیرهایی که برای آزمودن آنها بکار گرفته میشوند.
نقش متغیرها در فرضیات: متغیرها، فرضیهها را بصورتی نشان میدهند که محققان رفتاری و مدیریتی بتوانند آنها (فرضیهها) را مشاهده و اندازه گیری نمایند.
انواع متغیرها:
• متغیر خصیصه: متغیری که مقدار آن از یک فرد به فرد دیگر و یا از یک عضو به عضو دیگر جامعه آماری ممکن است تغییر کند . مثل اندازه سازمان، قد افراد، رنگ چشم افراد، نظر آنها در مورد یک موضوع خاص و ..
• متغیر مستقل: به علت احتمالی یا فرضی متغیر وابسته، متغیر مستقل یا متغیر درونداد و به عبارتی محرک گفته میشود .
مثال: فرض کنید میخواهیم تاثیر مصرف شیر را روی افرایش قد افراد بررسی کنیم در این حالت مصرف شیر روی افزایش قد تاثیر دارد ولی افزایش قد روی مصرف شیر تاثیر ندارد بنابراین متغیر مستقل مصرف شیر است.
• متغیر وابسته: به متغیری که به تبع تغییر متغیر مستقل، مقدارش کم و زیاد میشود متغیر وابسته، متغیر پاسخ و یا برونداد اطلاق میشود. مثال: در مثال قبل افزایش قد از آنجایی که وابسته به مصرف شیر است به عنوان متغیر وابسته شناخته میشود.
• متغیر تعدیل کننده ( واسطهای ): متغیر ثانوی است که پژوهشگر میخواهد تاثیر آن را در متغیر مستقل اولیه و متغیر وابسته ملاحظه کند. این متغیر بدین منظور انتخاب میشود که روشن شود آیا این متغیر، رابطه بین متغیر مستقل و متغیر وابسته را تحت تأثیر قرار میدهد یا نه.
• متغیر کنترل: به متغیرهایی که در موقع انجام پژوهش، لازم است تأثیر آنها خنثی شده و یا از بین برود، متغیرهای کنترل میگویند.
فرق متغیر تعدیل کننده با متغیر کنترل
موقع انجام تحقیق، پژوهشگر سعی میکند تأثیرات متغیر کنترل را از بین ببرد ولی تأثیرات متغیر تعدیل کننده را مورد بررسی قرار میدهد.
مقیاسهای اندازه گیری متغیرها
1- ( Nominal scale ) مقیاس اسمی
2- مقیاس ترتیبی ( رتبه ای) ( Rank scale )
3- ( Interval scale ) مقیاس فاصله ای
4- (Ratio scale ) مقیاس نسبی
• مقیاس رسمی یا طبقهای: در این نوع مقیاس محققین از اعداد یا سمبولها صرفا برای طبقه بندی اشیا، اشخاص یا خصوصیات استفاده میکنند.
مثال: در مورد جنسیت ممکن است عدد 1 را برای مرد و عدد 2 را برای زن انتخاب کنیم ولی این ارقام مفهومی از رتبه را در برندارند.
• مقیاس ترتیبی: اگر صرف نظر از تفاوت محتویات یک طبقه با طبقه دیگر، یک نوع ارتباط بین آنها برقرار باشد در آن صورت میگویند متغیر مورد نظر دارای مقیاس ترتیبی است. به طور مثال در طیف لیکرت
• مقیاس فاصله ای: در مقیاس ترتیبی زمانی که فاصله بین دو طبقه نیز برای ما اهمیت داشته و به طور دقیق قابل اندازه گیری باشد. در این حالت به آن مقیاس فاصلهای گویند. در این نوع اندازه گیری نسبت هر دو فاصله، مستقل از واحد اندازه گیری و مستقل از نقطه صفر است.
مقیاس نسبی: مقیاسی است که علاوه بر داشتن همه خصوصیات مقیاس فاصله ای، دارای نقطه صفر واقعی نیز هست، مثل پوند و گرم
جدول مقادیر مقیاسهای چهارگانه
فرضیه
عبارتی آزمایشی است که رابطه بین دو یا چند متغیر که بصورت دقیق و روشن بیان میکند و پس از آزمایش، صحت یا سقم آن مشخص میشود.
ویژگیهای یک فرضیه خوب
1- واضح و بدون ابهام (بیان در قالب جملات خبری )
2- قابل تبیین ( علت یابی )
3- بیان کننده رابطه مورد انتظار بین متغیرها
4- قابل آزمون بودن ( آزمون پذیری )
انواع فرضیههای پژوهشی
1-فرضیههای توصیفی در مقابل فرضیههای استنباطی
2- فرضیههای تک متغیره در مقابل فرضیههای چندمتغیره
3-فرضیههای همبستگی در مقابل فرضیههای تجربی
4- فرضیههای پژوهشی با گروههای زوج شده در مقابل فرضیههای مستقل
5- فرضیههای پارامتریک در مقابل ناپارامتریک
فرضیه توصیفی درمقابل فرضیه استنباطی
فرضیه توصیفی فرضیهای است که در مورد کل جامعه آماری تدوین شده بعبارتی ادعایی را در مورد کل جامعه آماری بیان مینماید. در حالی که فرضیه استنباطی به فرضیهای اطلاق میشود که در مورد یک نمونه انتخابی از کل جامعه آماری تدوین شود و صحت و سقم آن تحت تأثیر خطای نمونه گیری است.
مثال: متوسط قد دانشجویان در ایران 160 است. اگر برای بررسی این فرضیه متوسط قد کل دانشجویان ایران اندازه گیری شود فرضیه مورد نظر، توصیفی است و اگر برای بررسی این فرضیه قد یک نمونه از دانشجویان اندازه گیری شود و براساس توزیع و در نظر گرفتن خطای نمونه گیری به آن پاسخ داده شود، فرضیه استنباطی است.
• فرضیه تک متغیره در مقابل چند متغیره
بر اساس تعداد متغیرهایی که در یک فرضیه حضور دارند آن را تک متغیره یا چند متغیره مینامند.
مثال: در فرضیه”قد دانشجویان در ایران 160 است” با توجه به اینکه تنها متغیری که در فرضیه حضور دارد قد دانشجویان است، فرضیه تک متغیره و در فرضیه “ بین انتخاب یک سیستم تشویقی مناسب برای کارکنان و افزایش کارایی سازمان رابطه معناداری وجود دارد. ” با توجه به آنکه دو متغیر “انتخاب یک سیستم تشویقی مناسب ”و “افزایش کارایی سازمان” در قرضیه حضور دارند فرضیه چند متغیره است.
• فرضیه همبستگی در مقابل فرضیه تجربی
در فرضیههای همبستگی و تجربی هدف بررسی وجود رابطه بین دو یا چند متغیر است با این تفاوت که در فرضیه همبستگی هیچ یک از متغیرهای مورد بررسی تحت کنترل پژوهشگر نیست ولی در فرضیههای تجربی حداقل یکی از متغیرها تحت کنترل پژوهشگر است.
مثال: بین تورم و نرخ بیکاری رابطه معناداری وجود دارد. در این فرضیه بررسی همبستگی بین دو متغیر مدنظر است، ( تورم و نرخ بیکاری) که هیچ یک تحت کنترل پژوهشگر نیست . پس فرضیه مورد نظر از نوع همبستگی است.
بین تغییر محل خدمت کارکنان از محل A به محل B و میزان کارایی آنها رابطه معنا داری وجود دارد. در این فرضیه نیز بررسی از نوع همبستگی است ولی انتخاب اینکه چه کارمندانی در محل A و کدام یک از کارمندان در محل B خدمت کنند در اخنیار پژوهشگر است بنابر این فرضیه از نوع تجربی است.
• فرضیه با گروههای جور شده در مقابل گروههای مستقل
در فرضیه با گروههای زوج شده، پژوهشگران یک گروه نمونه دارند که در آن هر آزمون شونده را از لحاظ یک متغیر واحد دو بار اندازه گیری میکنند ولی در فرضیه با گروههای مستقل، محقق برای آزمون، دو گروه دارد که هر کدام از آنها را از لحاظ یک متغیر واحد مشابه یک بار بطور جداگانه اندازه گیری مینماید.
مثال: استفاده از سیستم آموزشی A بر روی کارایی کارمندان اثر مثبت دارد. برای بررسی چنین فرضیهای یک گروه از کارمندان انتخاب شده و کارایی آنها قبل و بعد از آموزش بررسی میشود و بین این دو دسته از اطلاعات بررسی انجام میشود. در این مورد ما تنها یک گروه داشتیم که به صورت قبل و بعد بررسی شدند پس فرصیه مورد نظر از نوع فرضیه با گروههای جور شده است.
کارایی کارکنان سازمان A بیشتر از کارایی کارکنان شرکت B است در این مورد ما دو دسته از افراد را مورد بررسی قرار میدهیم بنابراین فرضیه بیان شده، فرضیه با گروههای مستقل است.
• فرضیههای پارامتریک در مقابل ناپارامتریک
فرضیههای پارامتری فرضیههایی هستند که در آنها از متغیرهای نسبی یا فاصلهای استفاده شده و توزیع جامعه (و یا نمونه ) نرمال میباشد. در مقابل فرضیههای ناپارامتریک، فرضیههایی هستند که متغیرهای موجود در آنها دارای مقیاس اسمی یا رتبهای میباشند یا این که بر اساس شواهد موجود، محققان نمیتوانند فرض نرمال بودن جامعه ( نمونه ) را بپذیرند.
تعریف آمار: روش علمی که جهت جمعآوری، تلخیص، طبقهبندی، تجزیه و تحلیل و تفسیر به کار میرود، به عبارت دیگر به بررسی و مطالعه مشاهدات به صورت علمی اشاره دارد به عبارت دیگر، به مشاهدات عددی و ارقام ریاضی اطلاق میشود مانند: آمارهای بانک مرکزی، گزارشهای آماری سازمانهای مختلف.
- کاربرد علم آمار
1- در علوم اجتماعی و رفتاری: این نوع کاربرد کمی قبل از جنگ جهانی دوم وارد علوم اجتماعی و رفتاری شد که کاربرد آن همچنان ادامه دارد.
2- بعد از جنگ جهانی و به منطور برآورد دقیق خسارات و خرابیها جنگ به منظور پیشبینی هزینههای بازسازی.
3- آمار در تبدیل دادهها به اطلاعات و تفسیر این اطلاعات به منظور افزایش دانش بشری سهم بسزایی دارد.
4- استفاده از آمار در حوزه مدیریت از جمله تکنیکهای شبیه سازی در رشته سیستمهای مدیریتی.
5- استفاده از نرمافزارهای آماری به منظور تجزیه و تحلیلها» spss«
6- به کارگیری فنون پایهای آمار در بررسی صحت و سقم فرضیههای علمی.
سیر تحول آمار از نظر موضوعی:
به طور کلی از این نظر آمار به 3 مرحله تقسیم میشود .
1- آمار توصیفی(Descriptive statistics): این آمار صرفا به توصیف جامعه میپردازند و هدف آن مصاحبههای پارامترهای جامعه است، چنانچه محاسبه مقادیر و شاخصهای جامعه آماری با استفاده از سرشماری تمام اعضای جامعه باشد به آن آمار توصیفی میگویند.
2- آمار استنباطی(Inferential statistics): چنانچه به جای مطالعه کل اعضای جامعه، بخشی از آن با استفاده از فنون نمونهگیری انتخاب شده، و مورد مطالعه قرار گیرد و بخواهیم نتایج حاصل از آن را به کل جامعه تعمیم دهیم از روشهایی استفاده میشود که موضوع آمار استنباطی است. آن چه که مهم است، این است که در گذر از آمار توصیفی به آمار استنباطی یا به عبارت دیگر از نمونه به جامعه بحث و نقش احتمال شروع میشود. در واقع احتمال، پل رابط بین آمار توصیفی و استنباطی به حساب میآید.
3- آمار ناپارامتریک(Nonparametric statistics): عبارت است از اینکه جامعه آماری ما دارای توزیع نرمال نیست.
جامعه آماری: به مجموعهای از اشیا یا افراد اطلاق میشود که میخواهیم در یک موضوع یا چند موضوع در مورد آ» مطالعه کنیم.
نمونه آماری: به تعدادی از اعضای جامعه آماری که دارای صفات یا ویژگیهای مشترک هستند میگویند و با n نشان میدهند.
انواع متغیرها در آمار:
تعریف متغیر: متغیر مقداری است که از یک فرد به فرد دیگر ممکن است تغییر کند. مثل اندازه سازمان که از کوچک به متوسط و سپس بزرگ تغییر میکند.
متغیرها به دو دسته تقسیم میشود:
1- متغیر کیفی: متغیری است که نتوان با اعداد و ارقام آن را نمایش داد، مثل: عدالت، شجاعت، ایثارگری
2- متغیر کمی: متغیری است که بتوان با اعداد و ارقام آن را نمایش داد، مثل: تعداد خانوارها، میزان حقوق دریافتی
انواع مقیاسها: در آمار به طور کلی مقیاسها را به 4 دسته تقسیم میکند:
انواع نمونه گیری:
نحوه جمع آوری اطلاعات:
انواع دادهها: دادهها را به دو دسته طبقهبندی میکند:
آمار استنباطی، یکی از مباحث مطرح در روانسنجی در علم روانشناسی بوده و به معنای ابزار و روشهایی است که برای خلاصه کردن و توصیف دادهها، دستورالعمل لازم را فراهم میسازند و روشهای لازم جهت تعمیم نتایج از گروههای آزمودنی به گروههای وسیعتر را تهیه کرده و برای گزینش آزمودنی و جایگزینی آنها در گروههای مختلف و جمعآوری دادهها دستورالعمل ارائه میکنند. در این مقاله بعد از بیان تعریف و کاربرد آمار استنباطی به بررسی مفاهیمی چون جامعه و نمونه، پارامتر و شاخص آماری، ویژگیهای برآوردکنندهها، آزمون فرض و ... میپردازیم.
مفاهیم و ابزارهای آماری به صورت صریح یا ضمنی بخشی از فرایند اکثر تحقیقات را شامل میشوند. نقش این مفاهیم و ابزارها را میتوان هنگام تصمیمگیری در مورد گزینش آزمودنیها، جایگزینی آنها در گروههای مختلف، توصیف دادههای جمعآوریشده و تعمیم یافتههای حاصل از مطالعه، مشاهده کرد. بنابراین در تحقیق رفتاری، روشهای آماری چندین نقش ایفا میکنند که با هم ارتباط دارند. روشهای آماری برای خلاصه کردن و توصیف دادهها دستورالعمل لازم را فراهم میسازند. همچنین روشهای لازم جهت تعمیم نتایج از گروههای آزمودنی به گروههای وسیعتر را تهیه کرده و برای گزینش آزمودنی و جایگزینی آنها در گروههای مختلف و جمعآوری دادهها دستورالعمل ارائه میکنند.
- ماهیت: نقش آمار توصیفی در واقع، جمعآوری، خلاصه کردن و توصیف اطلاعات کمّی به دستآمده از نمونهها یا جامعهها است. اما محقق معمولا کار خود را با توصیف اطلاعات پایان نمیدهد، بلکه سعی میکند آنچه را که از بررسی گروه نمونه به دست آورده است به گروههای مشابه بزرگتر تعمیم دهد. تئوریهای روانشناسی از طریق تعمیم نتایج یک یا چند مطالعه به آنچه که ممکن است در مورد کل افراد جامعه صادق باشد به وجود میآیند.
از طرف دیگر در اغلب موارد مطالعه تمام اعضای یک جامعه ناممکن است. از اینرو محقق به شیوههایی احتیاج دارد که بتواند با استفاده از آنها نتایج به دستآمده از مطالعه گروههای کوچک را به گروههای بزرگتر تعمیم دهد. به شیوههایی که از طریق آنها ویژگیهای گروههای بزرگ براساس اندازهگیری همان ویژگیها در گروههای کوچک استنباط میشود آمار استنباطی گفته میشود.
به بیان دیگر، در پژوهشهای روانشناسی و سایر علوم رفتاری کسب اطلاعات درباره گروههای کوچک غالبا هدف پژوهشگر نیست، بلکه او علاقمند است که از طریق یافتههای این گروه کوچک، اطلاعات لازم را درباره جامعهای که این گروه کوچک را از آن انتخاب کرده است، کسب کند. یعنی در این پژوهشها هدف پژوهشگر تعمیم نتایج بهدستآمده از یک گروه کوچک به یک جامعه بزرگتر میباشد. این تعمیم مستلزم آن است که پژوهشگر از روشهای آماری پیشرفتهتری تحت عنوان "استنباط آماری" استفاده نماید.
- جامعه و نمونه: در مدل استنباط آماری، فرض بر این است که میخواهیم در مورد یک مجموعه خیلی بزرگ (شاید نامحدود)، اطلاعات کسب کنیم (مثلا نمره پیشرفت تحصیلی درس ریاضی دانشآموزان کلاس پنجم دبستان در سراسر کشور). به این مجموعه، جامعه گفته میشود. گاه حجم جامعه آنقدر بزرگ است که نمیتوان تمام آن را مطالعه نمود، لذا از کل مجموعه، یک زیرمجموعه به عنوان نمونه کل مشاهدات ممکن برای مطالعه انتخاب میشود.
به این زیرمجموعه که شامل تعداد محدودی از اعضای جامعه است "نمونه" گفته میشود. اما جهت استنباط خصوصیات جامعه از روی خصوصیات نمونه، مدل آماری ایجاب میکند که اعضای گروه نمونه بهصورت تصادفی انتخاب شوند. نمونه تصادفی به نمونهای گفته میشود که همه اعضای جامعه به یکاندازه شانس شرکت و انتخاب شدن در آن را داشته باشند. همچنین انتخاب هر فرد مستقل از افراد دیگر صورت گیرد.
- پارامتر و شاخص آماری: برای استنباط در مورد یک جامعه، محقق خصوصیات جامعه (مثلا مقادیر مرکزی یا شاخصهای پراکندگی) را با استفاده از خصوصیات گروه نمونه توصیف میکند. به مقادیری که خصوصیات جامعه (مثل میانگین یا واریانس) را توصیف میکنند، پارامتر گفته میشود. به مقادیری هم که خصوصیات نمونه را توصیف میکنند، آماره یا شاخص آماری میگویند.
برای تمییز قائل شدن بین دو مفهوم پارامتر و شاخص آماری معمولا پارامترها را با حروف یونانی و شاخصهای آماری را با حروف لاتین نمایش میدهند. به عنوان مثال برای نمایش دادن میانگین جامعه از حرف یونانی (مو = µ) و برای نشان دادن میانگین گروه نمونه از حرف لاتین ۱۲X' type="#_ x۰۰۰۰_ t۷۵"> (بخوانید ایکسبار) و برای نشان دادن واریانس جامعه از حرف یونانی ۲σ (مجذور زیگما) و برای نشان دادن واریانس نمونه از ۲S استفاده میشود.
- ویژگیهای برآوردکنندهها: از آنجا که اندازهگیری پارامترها (به خاطر حجم بزرگ جامعه و هزینههای بالا) عملا ناممکن است، این پارامترها با استفاده از آمارهها یا شاخصهای آماری، برآورد میشوند. اما چون نمونه فقط بخش کوچکی از یک جامعه را تشکیل میدهد، احتمال مساوی بودن آمارهها با پارامترها کم است. به عنوان مثال، اگر چه ۱۲X' type="#_ x۰۰۰۰_ t۷۵">به عنوان بهترین برآوردکننده µ بهشمار میرود، ولی این برآورد معمولا با مقداری خطا همراه است. این خطا ناشی از عوامل تصادفی بیشماری است که محقق از وجود آنها بیاطلاع است. برآوردکنندهها سه ویژگی عمده دارند:
· غیر سودار بودن: برآوردکنندهای غیر سودار است که اگر تعداد بینهایت نمونه به صورت تصادفی از یک جامعه انتخاب شود، میانگین آن در تمام نمونهها با مقدار پارامتر برآورد شده برابر باشد.
· یکنواخت بودن: منظور از یکنواخت بودن برآوردکننده آن است که هر چه تعداد یا حجم نمونه افزایش یابد، مقدار برآوردشده به مقدار پارامتر جامعه نزدیک و نزدیکتر گردد.
· کارا بودن: کارآیی برآوردکننده عبارت است از مقدار تغییر در برآورد پارامترهای جامعه از یک نمونه به نمونه دیگر. یعنی دقت برآوردکننده در پارامتر جامعه را کارآیی برآوردکننده مینامند.
البته باید توجه داشت که یک برآوردکننده ممکن است یک، دو یا هر سه خصوصیت را دارا باشد.
- آزمون فرض: فرض آماری، ادعایی در مورد یک یا چند جمعیت مورد بررسی است که ممکن است درست یا نادرست باشد. به عبارت دیگر فرض آماری، یک ادعا یا گزارهای در مورد توزیع یک جمعیت یا پارامتر توزیع یک متغیر تصادفی است. فرضیه آماری، نقطه آغاز آزمون فرض است و اصولا بدون داشتن فرضیه آماری امکان انجام یک آزمون دشوار است.
فرضیه آماری به دو نوع فرض صفر (H۰) و فرض خلاف (HA) بیان میشود. فرضیهای که در آزمونهای آماری مورد آزمون قرار میگیرد فرضیه صفر است که همیشه حاکی از عدم وجود تفاوت میباشد. اما فرض خلاف همان فرضیه پژوهشی است که میتواند جهتدار یا غیر جهتدار باشد. البته انتخاب فرضیه جهتدار دلخواه و تصادفی نیست، بلکه در صورتی فرضیه پژوهشی را میتوان جهتدار تدوین کرد که تئوری یا تحقیقات قبلی شواهدی برای آن ارائه کنند.
- انواع خطا: پس از انجام آزمونهای آماری، محقق در مورد رد یا عدم رد فرضیه صفر تصمیم میگیرد. اگر نتایج آزمون به گونهای باشد که نتوان آن را رد کرد، جایی برای اثبات یا تایید فرضیه پژوهشی باقی نمیماند، اما اگر فرضیه صفر رد شود، بهطور غیرمستقیم فرضیه پژوهشی تایید میشود. اگر فرضیه صفر در واقع صحیح باشد ولی محقق تصمیم به رد آن بگیرد خطای نوع اول رخ داده است. بر عکس اگر فرضیه صفری در واقع فرضیهای غیرصحیح باشد ولی محقق آن را تایید کند، دچار خطای نوع دوم شده است.
- آزمونها: آزمونهای آماری مورد استفاده جهت تجزیه و تحلیل اطلاعات به دستآمده از یک گروه کوچک (نمونه) و تعمیم آن به جامعه مورد نظر با توجه به مقیاس اندازهگیری متغیرها، به دو گروه "پارامتریک" و "ناپارامتریک" تقسیم میشوند. آزمونهای پارامتریک، به تجزیه و تحلیل اطلاعات در سطح مقیاس فاصلهای و نسبی میپردازند که حداقل شاخص آماری آنها میانگین و واریانس است. در حالی که آزمونهای ناپارامتریک، به تجزیه و تحلیل اطلاعات در سطح مقیاس اسمی و رتبهای میپردازند که شاخص آماری آنها میانه و نما است.
...
...
...
آمار پارامتریک و ناپارامتریک اشاره به روشهایی دارند که برای آزمون فرضیهها یا پاسخ به پرسشهای پژوهش در آمار کاربردی مدیریت و آمار استنباطی استفاده میشوند. منظور از آمار استنباطی، برآورد ویژگی جامعه (پارامتر) براساس مقادیر نمونه (آماره) است. از آنجا که استنباط آمارشناسان از جامعه تنها بر خصائص نمونه استوار است بنابراین تغییرپذیری میانگین نمونهها ظاهرا به صورت یک مشکل جدی به نظر میرسد اما چون ماهیت آنها مشخص است برآورد تغییر پذیری میانگین نمونهها براساس احتمالات از طریق اجرای آزمونهای آماری امکان پذیر خواهد بود.
آزمونهای آماری روشهایی هستند که به منظور بررسی میزان دقت و اعتبار دادههای آماری و یا به بیان دیگر تعیین میزان تاثیر خطای نمونهگیری در برآورد پارامتر جامعه براساس شاخصهای آماری نمونه بکار میروند. این آزمونها بهطور کلی به دو دسته تقسیم میشوند:
آمار پارامتریک Parametric statistics
آمار ناپارامتریک Non-parametric statistics
آزمونهای پارامتریک و پیشفرضهای مربوط به آن
آزمونهای پارامتریک را میتوان از موثرترین آزمونها دانست که در قالب موارد در تعمیم نتایج حاصل از گروه نمونه به جامعه آماری مورد استفاده قرار میگیرند. مشروط بر اینکه پیشفرضهای زیر در مورد آنها رعایت شوند:
۱- هریک از موارد مشاهده شده مستقل است یعنی انتخاب یک مورد به انتخاب هیچ مورد دیگری وابسته نیست.
۲- واریانس نمونهها برابر یا تقریباً برابر است. رعایت این نکته در نمونههای با حجم کم اهمیت بیشتری دارد.
۳- توصیف متغیرها براساس مقیاسهای نسبی و یا فاصلهای انجام میگیرد.
آزمونهای ناپارامتریک
گاهی در پژوهشها، دادههایی گردآوری میشوند که دارای مقیاس اسمی یا رتبهای میباشند. همچنین ممکن است دادهها دارای مقیاس فاصلهای باشند ولی توزیع دادهها در جامعه طبیعی (نرمال) نیست. در چنین مواردی پژوهشگر ملزم به استفاده از آزمونهای ناپارمتریک است. این آزمونها در کلیه مواردی که پژوهشگر نمیتواند از آزمونهای پارامتریک استفاده کنید ابزار مناسبی برای آزمون فرضیهها هستند. بطورکلی میتوان گفت که این آزمونها در مورد دادههایی بکار میروند که:
۱- مقیاس اندازهگیری آنها اسمی یا رتبهای باشد (از نوع دادههای ناپیوسته و یا منفصل و بنابراین حاصل شمارش هستند).
۲- بر نرمال بودن توزیع در جامعه استوار نیستند.
سوالات کلیدی
دادههای من نرمال است آیا میتوانم از روشهای ناپارامتریک استفاده کنم؟
بطورکلی آمار ناپارامتریک به نرمال بودن یا نبودن توزیع دادهها حساس نیست و در هر شرایطی قابل استفاده است. این نوع آمار در مقابل آمار پارامتریک بیان میشود. فرض اساسی در آمار پارامتریک برخوردار بودن مشاهدات از توزیع نرمال است. در حالیکه در فنون ناپارامتریک این فرض ضرورتی ندارد. در بخش اعظم تحقیقات مدیریت که بیشتر متغیرهای آن با مقیاسهای کیفی سنجیده میشود از این فنون استفاده میشود. این متغیرها فاقد توزیع آماری هستند و آنها را آزاد از توزیع Free of distribution میخوانند.
چرا همیشه از روشهای ناپارامتریک استفاده نمیکنیم؟
اگر روشهای ناپارامتریک همیشه قابل استفاده است و برای دادههای نرمال نیز میتوان از آن استفاده کرد پس چرا همیشه از روشهای ناپارامتریک استفاده نکنیم؟ علت اصلی آن است که روشهای پارامتریک نتایج دقیقتر و درستتری را ارائه میکنند بنابراین اگر شرایط مهیا بود و دادهها نرمال بودند بهتر است از روشهای پارامتریک استفاده شود.
انواع آزمون پارامتریک و ناپارامتریک
الف) آزمونهای میانگین جامعه
انواع آزمون میانگین جامعه از روشهای پرکاربرد در مدیریت میباشند.
یک میانگین از یک جامعه
مثال: بررسی رضایت دانشجویان مدیریت از سایت پارسمدیر
روش پارامتریک: آزمون t تک نمونه
روش ناپارامتریک: آزمون علامت تک نمونه و آزمون دوجملهای (نسبت موفقیت)
یک جامعه و یک میانگین
یک میانگین از یک جامعه
دو میانگین از یک جامعه
مثال: بررسی اختلاف میانگین رضایت دانشجویان پیش و پس از ارتباط با سایت پارسمدیر
روش پارامتریک: آزمون t زوجی
روش ناپارامتریک: آزمون علامت زوجی و آزمون ویلکاکسون
دو میانگین از یک جامعه
دو میانگین از یک جامعه
یک میانگین از دو جامعه
مثال: بررسی اختلاف میانگین رضایت دانشجویان دختر و پسر از سایت پارسمدیر
روش پارامتریک: آزمون t مستقل
روش ناپارامتریک: آزمون U مان-ویتنی
یک میانگین از دو جامعه
یک میانگین از دو جامعه
یک میانگین از چندجامعه
مثال: بررسی اختلاف میانگین رضایت دانشجویان رشتههای مختلف از سایت پارسمدیر
روش پارامتریک: آزمون آنالیز واریانس ANOVA
روش ناپارامتریک: آزمون H کروسکال-والیس
یک میانگین از چند جامعه
یک میانگین از چند جامعه
ب) آزمونهای همبستگی
انواع تحقیق همبستگی و رگرسیون دومین دسته از روشهای پرکاربرد آمار در مدیریت میباشند.
همبستگی ساده
مثال: بررسی رابطه میان اعتماد، رضایت و وفاداری دانشجویان مدیریت به سایت پارسمدیر
روش پارامتریک: آزمون همبستگی پیرسون
روش ناپارامتریک: آزمون همبستگی اسپیرمن و آزمون همبستگی تاو کندال
رگرسیون
مثال: بررسی تاثیر رضایت بر اعتماد و وفاداری دانشجویان مدیریت به سایت پارسمدیر
روش پارامتریک: رگرسیون خطی یا چندگانه
روش ناپارامتریک: رگرسیون ناپارامتری
مدل معادلات ساختاری
مثال: بررسی تاثیر رضایت بر اعتماد و وفاداری دانشجویان مدیریت به سایت پارسمدیر
روش پارامتریک: مدل معادلات ساختاری
روش ناپارامتریک: حداقل مربعات جزئی
نتیجهگیری بحث آمار پارامتریک و ناپارامتریک
برای آنکه براساس دادههای گردآوری شده از نمونه بتوانیم مقدار پارامتر جامعه را برآورد کنیم از روشهای آمار استنباطی استفاده میشود. آمار استنباطی خود براساس دو روش پارامتریک و ناپارامتریک قابل انجام است. در روشهای پارامتریک باید پیشفرضهایی وجود داشته باشد که مهمترین آنها نرمال بودن دادهها است. این روشها به نتایج دقیقتری میرسند و از پشتوانه آماری قویتری برخوردار هستند اما در بسیاری موارد شرایط انجام آنها وجود ندارد. در چنین شرایطی باید از روشهای آماری ناپارامتریک استفاده شود. انواع مختلفی از آزمونهای آماری برای بررسی میانگین جامعه، رگرسیون، همبستگی و مدلهای معادلات ساختاری وجود دارد. بسته به شرایط پژوهش و اقتضائات خاص آن و همچنین نوع دادههای گردآوری شده میتوان از روشهای مختلف آماری استفاده کرد.
از پرکاربردترین آزمونهای پارامتریک میتوان به آزمون t و آزمون تحلیل واریانس اشاره کرد. آزمون t، توزیع یا در حقیقت خانوادهای از توزیعها است که با استفاده از آنها فرضیههایی که درباره نمونه در شرایط جامعه ناشناخته است، آزمون میشود.
اهمیت این آزمون (توزیع) در آن است که پژوهشگر را قادر میسازد با نمونههای کوچکتر (حداقل ۲ نفر) اطلاعاتی درباره جامعه به دست آورد. آزمون t شامل خانوادهای از توزیعها است (برخلاف آزمون z) و اینطور فرض میکند که هر نمونهای دارای توزیع مخصوص به خود است و شکل این توزیع از طریق محاسبه درجات آزادی (Degrees of Freedom) مشخص میشود. به عبارت دیگر توزیع t تابع درجات آزادی است و هرچه درجات آزادی افزایش پیدا کند به توزیع طبیعی نزدیکتر میشود.
از سوی دیگر هرچه درجات آزادی کاهش یابد، پراکندگی بیشتر میشود. خود درجات آزادی نیز تابعی از اندازه نمونه انتخابی هستند. هرچه تعداد نمونه بیشتر باشد بهتر است. از آزمون t میتوان برای تجزیه و تحلیل میانگین در پژوهشهای تکمتغیری یکگروهی و دوگروهی و چند متغیری دوگروهی استفاده کرد.
زمانی که پژوهشگری بخواهد بیش از دو میانگین (بیش از دو نمونه) را با هم مقایسه کند، باید از تحلیل واریانس استفاده کند. تحلیل واریانس روشی فراگیرتر از آزمون t است و برخی پژوهشگران حتی وقتی مقایسه میانگینهای دو نمونه مورد نظر است نیز از این روش استفاه میکنند.
طرحهای متنوعی برای تحلیل واریانس وجود دارد و هر یک تحلیل آماری خاص خودش را طلب میکند. از جمله این طرحها میتوان به تحلیل یکعاملی واریانس (تحلیل واریانس یکراهه) و تحلیل عاملی متقاطع واریانس، تحلیل واریانس چندمتغیری، تحلیل کوواریانس یکمتغیری و چندمتغیری و... اشاره کرد.
-آزمون t تک نمونهای (تک گروهی)
-آزمون t مستقل
-آزمون t وابسته
-تحلیل واریانس یکطرفه
-تحلیل واریانس یک عاملی برای k گروه وابسته یا طرح اندازهگیریهای مکرر
-تحلیل واریانس دوطرفه یا طرح دو عاملی
-تحلیل کوواریانس
تحلیل واریانس (Analysis of Variance یا ANOVA) یک روش آماری است که برای مقایسه میانگین بین سه یا بیشتر گروه از دادهها استفاده میشود. هدف اصلی ANOVA، بررسی این است که آیا میانگین متغیر وابسته (مثلاً امتیازات، فروش، زمان و غیره) بین گروههای مختلف متفاوت است یا خیر
تحلیل واریانس (ANOVA) به چندین نوع تقسیم میشود که هر کدام برای موقعیتها و شرایط آماری خاص خود مناسب هستند. انواع مهم تحلیل واریانس عبارتند از:
1. One-way ANOVA (تحلیل واریانس یک عاملی)
یکی از رایجترین انواع ANOVA است که برای مقایسه میانگین بین سه یا بیشتر گروه (عامل) مستقل استفاده میشود. به طور معمول، یک عامل دارای سه یا بیشتر سطح (گروه) است که میخواهیم ببینیم آیا میانگین متغیر وابسته بین این گروهها متفاوت است یا خیر.
2. Two-way ANOVA (تحلیل واریانس دو عاملی)
در این نوع از ANOVA، دو عامل مستقل (factor) به عنوان متغیرهای مستقل در نظر گرفته میشوند و بررسی میشود که آیا هر کدام از این عوامل یا ترکیب آنها باعث تغییر در متغیر وابسته میشود یا خیر. این نوع ANOVA میتواند تأثیر تعاملی بین دو عامل را نیز بررسی کند.
3. ANCOVA (Analysis of Covariance)
تحلیل واریانس با کنترل متغیر تکوینی (Covariate) به عنوان یک متغیر تکوینی در ANCOVA در نظر گرفته میشود و بررسی میشود که آیا تفاوتهای میان گروهها در متغیر وابسته پس از کنترل بر متغیر تکوینی باقی میماند یا خیر.
4. MANOVA (Multivariate Analysis of Variance)
MANOVA از ANOVA برای بررسی تفاوتها در بیش از یک متغیر وابسته به یکباره استفاده میکند. به جای مقایسه میانگینها در هر متغیر وابسته به طور جداگانه، MANOVA اجازه میدهد تا همه متغیرهای وابسته را با هم در نظر بگیرد و تفاوتهای همزمان در این متغیرها را بررسی کند.
5. Repeated Measures ANOVA
این نوع از ANOVA برای بررسی تفاوتها در متغیرهای وابسته در طول زمان یا شرایط مختلف در یک گروه افراد استفاده میشود. به عنوان مثال، اثر یک درمان در طول زمان بررسی میشود و چگونگی تغییر در متغیرهای وابسته با توجه به زمان نمایش داده میشود.
6. Mixed-design ANOVA
این نوع ANOVA اجازه میدهد تا تأثیر عاملهای دوعاملی (between-subjects factors) و عامل تکرار (within-subjects factors) را در یک مطالعه بررسی کند. این نوع میتواند ارتباط بین افراد و شرایط مختلف را بررسی کند و تأثیر آنها را بر متغیر وابسته مورد ارزیابی قرار دهد.
هر کدام از این انواع ANOVA برای شرایط آماری خاص و سوالات پژوهشی خاص مناسب است. انتخاب نوع صحیح ANOVA بستگی به طرح پژوهش، تعداد عوامل مورد بررسی و نوع متغیرهای مورد مطالعه دارد.
در صورتی که شرایط استفاده از آزمونهای پارامتریک وجود نداشته باشد، برای مقایسه میانگین در یک یا چند گروه، از آزمونهای ناپارامتریک برای فرضیههای تفاوتی استفاده میشود. به عبارت دیگر، اگر متغیرها از نوع اسمی و رتبهای باشند یا اگر متغیرها از نوع فاصلهای و نسبی بوده ولی توزیع آماری جامعه نرمال نباشد، از روشهای ناپارامتریک استفاده میشود.
در پژوهشهایی که در سطح مقیاسهای اسمی و رتبهای اجرا میشوند، باید از آزمونهای ناپارامتریک برای تجزیه و تحلیل اطلاعات استفاده شود.
براساس نوع تحلیل (نیکویی برازش، همسویی دو نمونه مستقل، همسویی دو نمونه وابسته، همسویی K نمونه مستقل و همسویی K نمونه وابسته) و مقیاس اندازهگیری میتوان دست به انتخاب زد.
از آزمونهای مورد استفاده برای پژوهشها در سطح اسمی میتوان به آزمون ۲χ، آزمون تغییر مک نمار، آزمون دقیق فیشر و آزمون کاکرن اشاره کرد.
از آزمونهای مورد استفاده برای پژوهشها در سطح رتبهای میتوان به آزمونهای کولموگروف – اسمیرونف، آزمون تقارن توزیع، آزمون علامت، آزمون میانه، آزمون Uمان – ویتنی، آزمون تحلیل واریانس دو عاملی فریدمن و... اشاره کرد.
آزمون مجذور خی (۲ χ) برای سنجش تفاوت فراوانی مشاهده شده و فراوانی مورد انتظار طبقات یک متغیر به کار برده میشود تا مشخص کند آیا تفاوت موجود معنیدار بوده یا ناشی از خطا یا تصادفی است. برای مثال فرض کنید یک بازازیاب معتقد است که میزان جذابیت ۴ برند گوشیهای هوشمند در بین مردم یکسان است. به همین منظور او از تعدادی از درباره اینکه کدام برند را ترجیح میدهند، سئوال میکند.
پیش فرضهای آزمون خیدو
۱- متغیرها باید به صورت طبقهای (در سطح اسمی) باشند.
۲- تعداد طبقات متغیر دو یا بیشتر باشد.
۳- مجموع فراوانیهای مورد انتظار با مجموع فراوانیهای مشاهده شده برابر باشد.
۴- فراوانی مورد انتظار بیش از ۲۰ درصد خانههای جدول کمتر از ۵ نباشد. اگر چنین باشد محقق باید خانههای مجاور را با هم ترکیب کند تا مقدار فراوانی مورد انتظار را به بیش از ۵ برساند.<div
۵- فراوانیها یا مشاهدات مستقل از یکدیگر باشند.
۶- دادهها از یک نمونه تصادفی انتخاب شده باشند.
آزمونهای ناپارامتریک برای فرضیههای تفاوتی، آزمون خیدو تک متغیره
تصمیمگیری: در صورتی که مقدار ۲ χ محاسبه (مشاهده) شده از ۲ χ بحرانی جدول بزرگتر یا مساوی باشد (یا ۰٫۰۵ > p-value)، فرض صفر رد و فرض خلاف تأیید میشود. بنابراین با اطمینان ۹۵ درصد میتوان نتیجه گرفت بین فراوانی مشاهده شده و فراوانی مورد انتظار طبقات متغیر مورد مطالعه تفاوت معنیداری وجود دارد.
آزمون u مان- ویتنی یک آزمون ناپارامتریک برای مقایسه رتبههای دو گروه مستقل است. در واقع از این آزمون زمانی استفاده میشود که مفروضههای آزمون t مستقل مانند یکسانی واریانسها یا نرمال نبودن توزیع دادهها رعایت نشده و مقیاس متغیر وابسته رتبهای باشد. برای مثال، با استفاده از آزمون u مان- ویتنی میتوانید بررسی کنید که آیا بین نگرش زنان و مردان نسبت به تبعیض در پرداخت دستمزد تفاوت وجود دارد؟ در اینجا نگرش نسبت به تبعیض در پرداخت دستمزد متغیر وابسته میباشد که در مقیاس رتبهای اندازهگیری شده است. جنسیت نیز متغیر مستقل است که دارای دو گروه زنان و مردان میباشد. در صورتی که متغیر وابسته یعنی نگرش در مقیاس فاصلهای و توزیع آن نرمال نباشد، نیز میتوانیم از این آزمون استفاده میکنیم.
فرضیههای صفر و خلاف به صورت زیر نوشته میشوند:
آزمونهای ناپارامتریک برای فرضیههای تفاوتی، فرمول محاسبه آزمون من ویتنی
توجه: در بعضی منابع مقدار حجم نمونه n2 وn1 را ۲۰ معرفی و در نظر گرفته اند.
تصمیمگیری:
-- اگر حجم نمونه در دو گروه کوچکتر یا مساوی ۸ باشد (۸ ≥ n2 وn1)، به جدول توزیع مراجعه میکنیم. در صورتی که مقدار محاسبه شده از مقدار بحرانی جدول کوچکتر باشد، (یا ۰٫۰۵ > p-value) فرض صفر رد و فرض خلاف تأیید میشود. بنابراین با اطمینان ۹۵ درصد میتوان نتیجه گرفت بین میزان متغیر مورد مطالعه در دو گروه تفاوت معنیداری وجود دارد.
-- اگر حجم نمونه در دو گروه بزرگتر از ۸ باشد (۸ < n2وn1)، توزیع تقریباً نرمال خواهد بود و برای تفسیر آن از جدول توزیع Z استفاده میشود. درصورتی که مقدار Z محاسبه شده بزرگتر یا مساوی Z جدول باشد (یا ۰٫۰۵ > p-value)، فرض صفر رد و فرض خلاف پذیرفته میشود. بنابراین با اطمینان ۹۵ درصد میتوان نتیجه گرفت بین میزان متغیر مورد مطالعه در دو گروه تفاوت معنیداری وجود دارد.
آزمون ویلکاکسون به بررسی تفاوت بین دو گروه جور شده یا یک گروه که دو بار مورد آزمون قرار گرفته است، میپردازد. از این آزمون زمانی استفاده میشودکه مفروضههای آزمون t وابسته مانند یکسانی واریانسها یا نرمال نبودن توزیع دادهها رعایت نشده باشد و متغیر وابسته پیوسته و حداقل در مقیاس رتبهای باشد. برای مثال، آیا میزان مصرف روزانه سیگار قبل و بعد از یک برنامه ۶ هفتهای هیپنوتیسم درمانی تفاوت دارد؟ در اینجا میزان مصرف روزانه سیگار متغیر وابسته است که در مقیاس رتبهای اندازه گیری شده و گروههای وابسته “قبل” و “بعد” از هیپنوتیسم درمانی میباشند.
فرضیههای بدون جهت H0 و H1 به صورت زیر نوشته میشوند:
آزمونهای ناپارامتریک برای فرضیههای تفاوتی، فرمول محاسبه آزمون ویلکاکسون
-- تصمیمگیری:
-- در صورتی که ۲۵≥N : اگر مقدار T محاسبه شده کوچکتر یا مساوی مقدار T بحرانی جدول مربوط به توزیع ویلکاکسون باشد (یا ۰۵/۰ > p-value)، فرض صفر رد و فرض خلاف پذیرفته میشود. بنابراین با اطمینان ۹۵ درصد میتوان نتیجه گرفت بین میزان متغیر مورد مطالعه در دو گروه تفاوت معنیداری وجود دارد.
-- در صورتی که ۲۵<N : مقدار T به Z تبدیل میشود. سپس با مقدار بحرانی جدول توزیع Z مقایسه و تفسیر میشود. یعنی درصورتی که مقدار Z محاسبه شده بزرگتر یا مساوی Z جدول باشد (یا ۰٫۰۵ > p-value)، فرض صفر رد و فرض خلاف پذیرفته میشود. بنابراین با اطمینان ۹۵ درصد میتوان نتیجه گرفت بین میزان متغیر مورد مطالعه در دو گروه تفاوت معنیداری وجود دارد.
آزمون کروسکال والیس یا آزمون H معادل ناپارامتریک تحلیل واریانس یکطرفه است که تفاوت رتبهای سه یا بیش از سه گروه مستقل را نشان میدهد. در واقع از این آزمون زمانی استفاده میشود که مفروضههای آزمون تحلیل واریانس یکطرفه مانند یکسانی واریانسها یا نرمال نبودن توزیع دادهها رعایت نشده باشد. مقیاس متغیر وابسته حداقل رتبهای و حداقل سه گروه مستقل با اندازه نمونه حداقل ۵ وجود داشته باشد.
برای مثال، شما میخواهید بررسی کنید که آیا وضعیت اجتماعی – اقتصادی افراد بر نگرش آنها نسبت به افزایش مالیات فروش تاثیر میگذارد. نگرش نسبت به افزایش مالیات فروش متغیر وابسته است که در مقیاس رتبهای اندازه گیری شده و وضعیت اجتماعی – اقتصادی متغیر مستقل میباشد که دارای سه سطح است: طبقه کارگر، طبقه متوسط و طبقه ثروتمند.
فرضیههای H0 و H1 به صورت زیر نوشته میشوند:
آزمونهای ناپارامتریک برای فرضیههای تفاوتی، فرمول محاسبه آزمون کروسکال والیس
تصمیمگیری: برای تفسیر نتایج آزمون کروسکال والیس دو حالت وجود دارد:
-- برای بیش از ۳ گروه و در هر گروه بیش از ۵ آزمودنی با استفاده از جدول خیدو
-- برای ۳ گروه و در هر گروه ۵ یا کمتر از ۵ آزمودنی با استفاده از جدول مقادیر بحرانی H
-- در صورتی که مقدار H محاسبه شده از مقدار مقدار بحرانی جدول بزرگتر یا مساوی باشد (یا ۰٫۰۵ > p-value)، فرض صفر رد و فرض خلاف تأیید میشود. بنابراین در فرضیه بدون جهت با اطمینان ۹۵ درصد میتوان گفت رتبهبندی متغیر مورد مطالعه در گروهها متفاوت است.
آزمون فریدمن برای مقایسه میانگین رتبهبندی گروههای مختلف (بیش از دو گروه وابسته) یا اولویت بندی متغیرها براساس بیشترین تأثیر بر متغیر وابسته به کار میرود. بنابراین گروهها باید از قبل جور شده باشند. یعنی آزمودنیهای یکسان (همتا شده) در سه موقعیت یا بیشتر شرکت میکنند. همچنین تعداد آزمودنیها در هر یک از گروهها برابر است که البته از معایب این آزمون به حساب میآید. آزمون فریدمن مشخص میکند که آیا میانگینها یا حاصل جمعهای رتبهها به طور معنیداری با یکدیگر تفاوت دارند یا خیر.
در صورتی که پیش فرضهای لازم برای انجام آزمونهای پارامتریک تحلیل واریانس دوطرفه یا تحلیل واریانس با اندازهگیریهای مکرر وجود نداشته باشد، از معادل ناپارامتریک آنها یعنی آزمون فریدمن استفاده میشود. این روش، مفروضهای درباره شباهت توزیع متغیر در ردیفهای مختلف ندارد. بهعلاوه، تعامل را مورد بررسی قرار نمیدهد، زیرا بدون اندازههای کمی، تعامل بیمعنی است.
برای مثال فرض کنید یک تحلیلگر بازاریابی معتقد است که اثربخشی نسبی سه نوع تبلیغ شامل ارسال پست الکترونیک، درج در روزنامه و مجله را مقایسه کند. این تحلیلگر یک آزمایش بلوکی تصادفی انجام میدهد و شرکت بازاریابی برای ۱۲ مشتری از همه انواع تبلیغات در طول یک دوره یک ساله استفاده و درصد پاسخ آنها را به هر یک از انواع تبلیغات در آن سال ثبت میکند. او برای تعیین اینکه آیا میانه اثر آزمایش برای هر یک از انواع تبلیغات متفاوت است یا نه از آزمون فریدمن استفاده میکند.
پیش فرضهای آزمون فریدمن
۱- مفروضههای یکسانی واریانسها یا نرمال نبودن توزیع دادهها رعایت نشده باشد.
۲- مقیاس متغیر وابسته حداقل رتبهای باشد.
۳- حداقل سه گروه وابسته وجود داشته باشد.
در آزمون فریدمن، فرضیههای صفر و خلاف غالباً به صورتهای زیر تنظیم میشوند.
آزمونهای ناپارامتریک برای فرضیههای تفاوتی، فرمول محاسبه آزمون فریدمن
تصمیمگیری: برای تفسیر نتایج آزمون فریدمن دو حالت وجود دارد:
-- در نمونههای کوچک یعنی برای ۳=k و ۹ تا ۲=N و نیز ۴=k و ۴ تا ۲=N از جدول فریدمن استفاده میشود.
-- وقتی k و N بزرگتر از مقادیر فوق باشد، آزمون فریدمن تقریباً دارای توزیعی برابر با خیدو با درجه آزادی ۱-df= k است. از اینرو برای آزمون H0 میتوان از جدول توزیع خیدو استفاده کرد.
در صورتی که مقدار ۲ χ محاسبه شده از مقدار ۲ χ بحرانی جدول بزرگتر یا مساوی باشد (یا ۰٫۰۵ > p-value)، فرض صفر رد و فرض خلاف تأیید میشود. بنابراین در فرضیه بدون جهت با اطمینان ۹۵ درصد میتوان نتیجه گرفت بین گروههای همتا در زمینه متغیر وابسته تفاوت وجود دارد یا حاصل جمعهای رتبهها به طور معنی داری با یکدیگر تفاوت دارند.
اول
واریانس:
برای پیدا کردن واریانس معمولا از روابط زیر میتوان استفاده کرد:
σ2 = ∑x2i −µ2x , σ2x = ∑(x2i −µ2 2x) برای دادههای طبقهبندی نشده
x
N N
f xi i2 2
σ2x = ∑ −µx , σ2x = ∑f (xi i −µx)2 :برای دادههای طبقهبندی شده
N N
مثال: با توجه به اطلاعات زیر واریانس را محاسبه کنید:
∑f xi i2 =1000 , µ =x 4 , N =50
σ2x = ∑f xi i2 −µ2x ⇒ 2
Nباتوجه به همین مثال انحراف معیار چقدر است؟
2σx = σ2x = 4 = با توجه به همین مثال ضریب پراکندگی را حساب کنید؟
σx = 2 =0 5/
C.V =
µx 4
همانطور که قبلا گفته شده است این پارامتر برای توزیعهای مناسب است که دنبالهها دارای مشاهدات اندکی است، به بیان ساده تر، در جدول طبقه بندی دادهها، طبقه اول و آخر آن باز است.
IQR = Q −Q دامنه میان چارکی
=SIQR انحراف میان چارکی
3Q = چارک سوم 1Q = چارک اول
نکته: برای بدست آوردن چارک اول یا سوم از فرمول زیر استفاده میکنیم:
aN
Md = Lmd + 4 −Fci−1×I
fi
Lmd = کران پایین طبقه شامل چارک اول یا سوم
=a چارک اول یا سوم
1−Fci= فراوانی مطلق ماقبل چارک اول یا سوم fi= فراوانی همان طبقه شامل چارک اول یا سوم I= فاصله طبقات
C-L fi Fci
≤ 5 2 2
5-8 10 12
8-11 25 37
11-14 23 60
14-17 15 75
≥17 5 80
مثال: با توجه به جدول زیر محاسبه کنید دامنه میان چارکی و انحراف چارکی
Q3 = aN4 = 3×80 = 60⇒ Md =11+ 6023−37×3 =11+ 3 =14
4
Q1 = aN4 = 1 80×4 = 20⇒ Md = 8+ 20 1225− ×3 = 8 96/
IQR = Q3 −Q1 =14−8 96/ = 5 04/ Q3 −Q1 = 14−8 96/ = 2 52/ SIQR =
2 2
تصحیح شپارد:
از آنجاکه در دامیانگین وقهبندی شده از نماینده طبقات در محاسبه میانگین و واریانس استفاده میکنیم معمولا اعداد به دست آمده با واقعیت اختلاف دارد، بنابراین جهت اصلاح این انحراف از رابطه زیر استفاده میکنیم:
σ =σ −c2 2x
1- متغیرها باید پیوسته باشند.
2- تعداد N دست کم 100 تا باشد.
3- تابع توزیع فراوانی از نوع متقارن یا تقریبا متقارن باشد.
مثال: اگر 100σ2x = و ضریب اطمینان 5=I باشد، محاسبه کنید مقدار تصحیح شپارد چقدر است؟
σ =σ −2c 2x I2 ⇒σ = − = − =2c 100 52 100 25 97 1/
12 12 12
مثال: فرض کنید 200=1Q3 =400 , Q مقدار IQR و SIQR را محاسبه کنید.
IQR =400 200 200− =
SIQR = Q3 −Q1 ⇒ 400 200− =
100
2 2
مثال: اندازه 30 میله آهنی بر حسب cmبه شرح زیر است، محاسبه کنید:
الف) پارامترهای پراکندگی ب) پارامترهای پراکندی
2 35/ 2 45/ 2 55/ 2 6/ 2 35/ 2 46/
4 2/
3 1/
6 1/ 3 7/
2 9/
5 1/ 5 3/
3 2/ 7 2/ 6 2/ 4 7/ 4 1/ 7 1/
5 1/ 3 6/ 3 5/
6 4/
2 3/
2 55/ 2 6/ 2 4/ 5 6/ 3 7/ 4 2/
C-L Fci xi xi2 f xi i2
µ = = =
/22 5 =( ) 3 30 = چارک سوم
4 4
aN
2 -2/9 11 11 2/45 6/002 66/022
3 -3/9 6 17 3/45 11/902 71/412
4 -4/9 4 21 4/45 19/802 79/208
5 -5/9 4 25 5/45 29/702 118/808
6 -6/9 3 28 6/45 41/602 124/806
7 -7/9 2 30 7/45 55/502 111/004
30 571/26
Md = md + 4 −Fci−1×I ⇒ Md = +5 22 5 21/ 4− ×1 5 0 375 5 375⇒ + / = /
fi
چارک اول aN = 1 30( ) = 7 5/
4 4
aN
−Fci−
Md = md + 4 1×I ⇒ 2+ 7 5/ 11−11× =1 1 681/
fi
IQR = Q3 −Q1 = 5 375/ −1 681/ = 2 694/
SIQR = 3 694/ =1 92/
پارامترهای تعیین انحراف از قرینگی:
گاهی به علت اینکه 2 یا چند جامعه آماری جامعه دیگر دارای پارامترهای مرکزی یکسان هستند، در این حالت تصمیم گیرنده معمولا از پارامترهای پراکندگی استفاده میکنند. در چنین حالتی نیز ممکن است پارامترهای پراکندگی جواب یکسان داشته باشد، بنابراین بهتر است از روابط زیر که به معروف به ضریب چولگی پیرسون م یباشد استفاده کرد که در اینجا به طور خلاصه بر 3 رابطه آن میپردازیم:
1)µx −MO = 3(µx −M )d 2)SK1 = µx σ−xMO 3)SK2 = 3(µxσ−xM )d
مثال: چنانچه در جامعه آماری 12Md =16 , µx = باشد، مقدار MO را محاسبه کنید.
µx −MO = 3(µx −M )d ⇒12−MO = 3 12 16( − ) ⇒12−MO = −12
⇒ −MO = −12 12− ⇒ −MO = −24 ⇒ MO = −24 ⇒ MO = 24
−1
مثال: چنانچه انحراف معیار، میاگین و مد به ترتیب 2MO = 8 , µx =16 , σx = باشد، ضریب چولگی پیرسون چقدر است؟
SK1 = µx σ−xMO = 162−8 = 4
توابع احتمال گسسته:
1- متغیر تصادفی گسسته:
ابتدا لازم است به چند مثال زیر توجه شود:
فرض کنید در برگزاری مسابقه فوتبال به شرط آفتابی بودن 10,000,000 ریال سود و اگر ابری باشد 5,000,000 ریال و اگر بارانی یا برفی باشد، سود صفر است. فضای نمونه و متغیر تصادفی را به طور ساده نشان دهید.
[ باران، برفی »سود=0«، ابری »سود=5,000,000«، آفتابی »سود=10,000,000«]=S
فرض کنید سکهای را 2 بار پرتاب میکنیم، فضای نمونه و متغیر تصادفی آن را به طور ساده نشان دهید و شیر مدنظر میباشد. H= شیر T= خط
TT TH HT HH
S = ↓ , ↓ , ↓ , ↓
0 1 1 2
X (TH) (TH,HT) (HH)
P(X=x) 0/25 0/5 0/25
:احتمال متغیر تصادفی
تابعی در صورتی احتمال است که 2 خاصیت زیر را داشته باشد:
1) ∑P(X = x) =1
2) تابع احتمال منفی نباشد.
مثال:
اگر احتمال پرتاب 2 سکه طبق جدول زیر باشد آیا تابع احتمال میباشد؟ چرا؟
=P(X = x) =0 25 0 5 0 25 1/ + / + / ∑ تابع احتمال منفی نمیباشد.
جایگشت:
Prn = n! :ترکیب Prn = n! :تبدیل
r!(n −r)! (n −r)!
مثال اگر تابع زیر را داشته باشیم، مطلوب است محاسبه کنید تابع احتمال است؟ چرا؟
4
P(X = x) = x x =0 1 2 3 4, , , ,
16
Prn = r!(nn!−r)! ⇒ P04 = 0 4 0!(16 )! = 161 Prn = r!(nn!−r)! = P14 = 1 4!(16 1)! = 164
Prn = r!(nn!−r)! = P24 = 2 4!(16 2)! = 166 Prn = r!(nn!−r)! = P34 = 3 4!(16 3)! = 164
Prn = n!−r)! = P44 = 16 = 161 161 +164 +166 +164 +161 = 1616 =1
r!(nبله، زیرا جمع ترکیبها برابر با یک است و تابع آنها منفی نمیباشد.
تابع توزیع/ تابع احتمال تجمعی:
X -2 0 3 5 10
P(X = x) 0/1 0/15 0/25 0/3 0/2
P(X ≤ x) 0/1 0/25 0/5 0/8 1
تابع توزیع تابعی است که به ازای جمیع مقادیر ممکن متغیر تصادفی (X) احتمال وقوع مقداری کوچکتر یا مساوی »x« را نشان میدهد. P(X ≤ x)
مثال: با توجه به مقادیر 10، 5، 3، 0، 2- و احتمالات از چپ به راست به ترتیب 1/، 51/0، 52/0، 03/0،
2/0، محاسه کنید تابع توزیع و مقدار 1 3F( ) , F( )
F( )1 = P(X ≤ =1) 0 25/
F( )3 = P(X ≤ =3) 0 5/
مثال تعداد تلویزیونهای فروخته شده فروشگاهی، در 120 روز به شرح جدول زیر است:
مطلوب است: محاسبه کنید: الف) تابع احتمال ب) تابع توزیع احتمال تجمعی
ج) احتمال اینکه یک روز به صورت تصادفی انتخاب شود، کمتر و یا 5 تلویزیون باشد چقدر است؟
X 2 3 4 5 6 7
P(X = x) 0/15 0/225 0/25 0/125 0/15 0/1
P(X ≤ x) 0/15 0/375 0/625 0/75 0/9 1
تعداد روزها تعداد فروخته شده /0 25= 30 /0 225= 27 /0 15= 18
120 120 120
15 =0 125/ 18 =0 15/ 12 =0 1/
120 120 120
f( )5 = P(X ≤ =5) 0 75/
مثال: در تابع زیر a را چنان کنید که بتوان آن را یک تابع احتمال دانست؟
f(x) = ax2 x =0 1 2 3 4, , , , f(x1 4→ ) = a ( ) 0 2+( )1 2+( )2 2+( )3 2+( ) ( )4 2 5 2
= + + + + + =a[0 1 4 9 16 25] a55 =1⇒ a = = 0 018/
مثال شرکت بیمه اطلاعات 60 روز تصادفات را چنین اعلام کرده است؟ الف) تابع احتمال و تابع توزیع تصادفات
X 0 1 2 3 4
P(X = x) 0/25 0/42 0/17 0/1 0/06
P(X ≤ x) 0/25 0/67 0/84 0/94 1
ب) اگر روزی از این 60 روز به طور تصادفی انتخاب کنیم احتمال اینکه در این روز کمتر از 4 تصادف رخ داده باشد چقدر است؟
جلسه سوم/ ابوالفضل ولدی/20
امید ریاضی (متغیر تصادفی):
x 100 200 300 400 500
f(x) 0/15 0/25 0/3 0/2 0/1
E(X) 15 50 90 80 50
امید ریاضی همان میانگین موزون است که احتمالات در آن نقش وزنها( ضرایب) را دارد، امید ریاضی را با علامت E(X) نشان میدهند و همانطور که میدانیم در میانگین موزون، دادهها را در ضرایب، ضرب و سپس حاصل را بر مجموع ضرایب تقسیم میکنیم ولی امید ریاضی چون مجموع احتمالات »1« است پس از ضرب احتمالات در متغیر تصادفی دیگر نیازی به تقسیم نمیباشد.
E(X) = ∑X.f(x)
مثال: شرکت تولیدکننده آبگرمکن تقاضاهای سالانه را همراه با اطلاعات مربوط در جدول زیر آورده است،امید ریاضی تقاضاها را به دست آورید.
E(X) =∑x.f(x) ⇒ (100 0 15× / )+(200 0 25× / )+(300 0 3× / )+(400 0 2× / )+(500 0 1× / )
x -2 1 3 5
f(x) 0/2 0/4 0/3 0/1
E(X) -0/4 0/4 0/9 0/5 1/4
E(X )2 0/8 0/4 2/7 2/5 6/4
= + + + + =15 50 90 80 50 285
خواص امیدریاضی:
جلسه چهارم/ ابوالفضل ولدی/22
امید ریاضی مانند میانگین دارای خواص زیر است:
1)E(a) = a 2)E(ax) = aE(X)
3)E(ax + b) = aE(X)+ b 4)E(xn) = ∑x .f(x)2
5)z = ax + by+c ⇒ E(z) = E(ax)+ E(by)+ E(c) ⇒ z = aE(x)+ bE(y)+c
مثال: تابع احتمال زیر مفروض است؛ محاسبه کنید:
E(X )2 (د E(−3x +2) (ج E( X)2 (ب E(X) (الف
E(X) = ∑x.f(x) ⇒ (−2 0 2× / )+(1 0 4× / )+(3 0 3× / )+(5 0 1× / )
(الف
= −0 4 0 4 0 9 0 5/ + / + / + / =1 4/ ب) E( x)2 = 2E(X) ⇒ 2×(1 4/ ) = 2 8/
ج) E(−3x +2) = −3E(X)+2⇒ −3×(1 4/ )+2 = −2 2/
د) E(X )2 = ∑x .f(x)2 ⇒(−2)2×0 2/ + ( )1 2×0 4/ + ( )3 2×0 3/ ) + ( )5 2×0 1/
=0 8/ +0 4/ +2 7/ +2 5/ = 6 4/
واریانس:
با توجه به فرمول پایین میتوان 3 خاصیت برای آن بیان کرد.
V(X) = E(X )2 −E(X) :خاصیت اول
V(X) = V(a) =0 :خاصیت دوم
V(ax) = a V(X)2 :خاصیت سوم
V(ax + b) = V(ax)+ V(b) = a V(X)2 +0
مثال: توزیع احتمال زیر مفروض است؛ محاسبه کنید:
V(−4x −3) (و V(X) (د E ( −3x + 7)2 (ج E(−3x + 7) (ب E(X) (الف
جلسه چهارم/ ابوالفضل ولدی/23
جواب قسمت »الف«:
x 2 4 6 8 10
f(x) 0/1 0/25 0/3 0/25 0/1
E(X) 0/2 1 1/8 2 1
E(X )2 0/4 /4 10/8 16 10
E(X) = ∑x.f(x) ⇒ (2 0 1× / )+(4 0 25× / )+(6 0 3× / )+(8 0 25× / )+(10 0 1× / ) =0 2/ + +1 1 8/ + + =2 1 6 :«جواب قسمت »ب
E(−3x + 7) = −3E(X)+ 7 ⇒ −3×( )6 + 7 = −11
جواب قسمت »ج :«
E ( −3x + 7)2 = E ( 7−3x)2⇒ E ( ) 7 2 −2 7 3( )( x)+(3x)2 = E 49−42x +9x2
= E(49)−E(42)×E(X)+ E( )9 ×E(X )2 = 49−252+ 370 8/ =167 8/
E(X )2 = ∑x .f(x)2 ⇒( )2 2×0 1/ + ( )4 2×0 25/ + ( )6 2×0 3/ + ( )8 2×0 25/ + (10)2×0 1/
=0 4/ +4+10 8/ +16+10= 41 2/ «: جواب قسمت »د V(X) = E(X )2 −E(X) = 41 2/ −6 = 35 2/
جواب قسمت »و :«
تابع احتمال توام:
جلسه چهارم/ ابوالفضل ولدی/24
i i
ب) احتمال اینکه P(X =1) باشد.
ج) احتمال اینکه P(x > y) باشد.
د) احتمال اینکه P(y ≥ x =1) باشد .
و) توزیع احتمال z = x + y
مثال: با توجه به تابع زیر احتمالات حاشیهای x,y را بنویسید.
مثال: در جعبهای 8 مهره وجود دارد که 2 تای آنها معیوب است. به طور تصادفی 3 تا از آنها را بیرون م یآوریم (x= تعداد مهرههای سالم و y= تعداد مهرههای معیوب در نظر گرفته شود)، مطلوب است: محاسبه کنید جدول تابع احتمال توام و احتمالات حاشیه x , y.
جلسه چهارم/ ابوالفضل ولدی/25
کواریانس چیست:
امید ریاضی تعریف میشود، کواریانس معیار عددی است که نوع و شدت رابطه خطی بین دو متغیر تصادفی را نشان میدهد و میتواند 3 حالت داشته باشد.
1) با افزایش یک متغیر،متغیر دیگری نیز افزایش یابد، در چنین حالتی مثبت است.
2) با افزایش یک متغیر، متغیر دیگر کاهش یابد، در این حالت کواریانس منفی است.
3) با کاهش یا افزایش یک متغیر،متغیر دیگر تغییری نکند، در این حالت کواریانس صفر میباشد.
کواریانس بین 2 متغیر را با نماد روبرو نشان میدهیم؛ COV(x,y) بنابراین میتوان رابطه زیر را برای به دست آوردن کواریانس بیان کرد؟
COV = E(xy)−E(x).E(y)
نکته: اگر کواریانس دو متغیر تصادفی صفر باشد،x,y به این معنی نیست که و متغیر مستقلند، ولی چنانچه دو متغیر مستقل باشند، حتما کواریانس آنها صفر است.
مثال: تابع احتمال توام 2 متغیر تصادفی x,y به صورت زیر است؛ کواریانس را پیدا کنید.
x.f(x) = −( 5 0 4× / )+(1 0 6× / ) = − +2 6 4=
E(x,y) =[(x−5 0,y )×0 3/ ]+[(x−5 1,y )×0 02/ ]+[(x COV = E(xy)−E(x).E(y) = 9 1 4 1/ − × /18 = 4 38/
مثال: فرض از 10 شرکت بزرگ مربوط به صنعتی خاص 3 شرکت دارای سود خالصی بیش از 1,500,000,000 ریال است. از این 10 شرکت 2 شرکت به طور تصادفی انتخاب شد. اگر متغیر تصادفی x نشان دهنده تعداد شرکتهای که سودی بیش از 1,500,000,000 ریال دارند و متغیر تصادفی y نشان دهنده تعداد شرکتهای باشد که سودی کمتر یا مساوی این مبلغ داشته باشند محاسبه کنید:
الف) تابع احتمال توام
ب) احتمال اینکه 2 شرکت انتخاب شد سودی بیش از 1,500,000,000 ریال داشته باشند.
ج) اگر بدانیم کمتر از 2 شرکت با سود بیش از 1,500,000,000 ریال انتخاب شدهاند احتمال اینکه دقیقا یک شرکت با سود کمتر یا مساوی 1,500,000,000 انتخاب شود، چقدر است؟
د) احتمال اینکه تعداد شرکتهای با سود بیش از 1,500,000,000 بیشتر از تعداد شرکتهایی با سود کمتر یا مساوی باشد چقدر است؟
و) تابع احتمال متغیر تصادفی x را بنویسید.
استقلال دو متغیر تصادفی:
همانطور که قبلا گفته شده است 2 پیشامد A و B در صورتی مستقلاند که رابطه زیر در مورد آنها صادق باشد.
P(A∩B) = P(A)×P(B)
با توجه به این رابطه میتوان برای تمام زوجهای (x ,yi i) بنویسیم f(x ,y )i i = xi ×yi همچنین در این قسمت میتوان به طور کلی رابطه زیر را بیان کرد.
غیرمستقلاند COV(xy) =0→ x,y توزیع برنولی:
چنانچه در آزمایشهای (مثل پرتاب سکه) دو پیامد وجود داشته باشد احتمال موفقیت و یا شکست هر پیامد ثابت باشد را توزیع برنولی میگویند و معمولا از رابطه: 1=p+q به دست میآید.
مثال: در جعبهای 20 کالا موجود است،5 تای آنها ناسالم است، احتمال خارج شدن یک کالای سالم چقدر است؟
p+q =1⇒ p = 15 , q = 5 :جواب
20 20
نکته: در این مثال چنانچه اولین کالای انتخاب شده (معیوب و سالم) انتخاب و مججدا به جعبه برگردانده شود در این صورت توزیع دیگر برنولی نمیباشد.
مثال: در کارتونی 3 کالای ناسالم و 27 سالم وجود دارد، کالاها را بدون جایگذاری انتخاب میکنیم، احتمال اینکه موفق شویم کالای سالم خارج کنیم چقدر است؟
p+q =1⇒ p = 27 , q = 3 :جواب
30 27
مثال: چنانچه از هر 100 نفر نوزاد متولد شده، به طور متوسط 48 دختر و بقیه پسر باشند. آیا این توزیع،توزیع برنولی است؟
جواب: 1= 52 + 48 ⇒1=p+q
100 100
مثال: یک میلیون نفر میخواهند به فردی از بین 5 نفر نماینده رای بدهند، برآورد چنین است که 500 هزار نفر به نفر سوم رای دهد موفقی این فرد چقدر است؟
جواب: با توجه به اینکه جامعه زیاد است، در چنین حالتی میتوان احتمال موفقیت را ثابت فرض نمود و نفر سوم رای میآورد و توزیع برنولی است.
توزیع 2 جملهای:
با احتمال موفقیت P توزیعی است که در آن متغیر تصادفی x م یتوان مقادیری از صفر الی بینهایت را انتخاب کند. به طور کلی میتوان فرمول زیر را برای آن نوشت:
n x n x−
p . q
x
مثال: محصلی میخواهد به 5 سوال دو گزینهای جواب دهد احتمال پاسخ دادن درست به هر سوال 7/0 است، احتمال اینکه دقیقا به 2 سوال پاسخ درست داده شود چقدر است؟ جواب:
n px . qn x− ⇒ P(X = x) = 5 ×(0 7/ )2×(0 3/ )5 2−
x 2
×0 49 0 027/ × / = 5× ×4 3!×0 49 0 027/ × / =10 0 49 0 027× / × / =0 1323/
2×3!
مثال: در جعبهای 6 مهره به ترتیب 5 مهره سفید و یک مهره سیاه وجود دارد، احتمال اینکه مهره سفید بیرون بیاید 17/0 است،احتمال اینکه دقیقا مهره سیاه بیرون بیاید چقدر است؟ جواب:
n = 6 , x =1 , p =0 17/ q =0 83/
P(X = x) = n px . qn x− ⇒ P(X = x) = 6 ×(0 17/ )1×(0 83/ )6 1−
x 1
⇒ ×0 17 0 393/ × / = 6 0 0668× / =0 40086/
مثال: از شرکتهای مورد حسابرسی قرار گرفته 25/0 آنها حسابهایشان رد شده است، اگر چهار شرکت بر حسب تصادف انتخاب کنیم احتمالات زیر را محاسبه کنید:
الف) حسابهای یک شرکت رد شده باشد ب) حسابهای دو شرکت رد شده باشد.
جواب قسمت »الف«:
n = 4 , x =1 , p =0 25/ , q =0 75/
P(X = x) = n px . qn x− ⇒ 4 ×(0 25/ )1×(0 75/ )4 1− = 4! ×0 25 0 421/ × / =0 421/
x 1 1 4!( −1)!
جواب قسمت »ب«:
n = 4 , x = 2 , p =0 25/ , q =0 75/
P(X = x) = n px . qn x− ⇒ 4 ×(0 25/ )1×(0 75/ )4 2− = 4! ×0 25 0 56/ × /
x 2 2 4!( −2)!
!
== 6 0 25 0 56× / × / =0 84/
جلسه پنجم/ ابوالفضل ولدی/30
نکته: گاهی اوقات در توزیع 2 جملهای صحبت بزرگ بودن n کار محاسباتی سخت میشود. در این صورت از جداول پیشبینی شده استفاده میشود.
مثال: 2/0 مصرفکنندگان پودرهای شوینده مصرفکننده مارک خاصی هستند اگر 17 مصرف کننده انتخاب شود احتمالات زیر چقدر است؟ الف) 3 مصرفکننده مشتری باشند.
ب) حداقل 4 مصرف کننده مشتری باشد.
ج) حداقل 2 و حداکثر 5 مصرفکننده مصرفکننده مشتری باشند.
تابع توزیع 2 جملهای منفی:
گاهی در توزیع برنولی به دنبال احتمال x موفقیت از n آزمایش هستیم که به آنها (k موفقیت اطلاق میشود) مثل اینکه پنجمین فردی که شایعهای را شنیده دومین فردی باشد که آنها را قبول کرده است.
به طور کلی در مورد این توزیع میتوان رابطه زیر را بیان کرد:
x −1 k x k−
P(X = x) = −1p . q
kx= تعداد آزمایشها k= تعداد موفقیتهای در x آزمایش
p= احتمال موفقیت در هر آزمایش q= احتمال عدم موفقیت در هر آزمایش واریانس و میانگین توزیع 2 جملهای منفی:
به طور خلاصه در 2 رابطه زیر بیان میشود:
k
مثال: احتمال یک دزدی در حین سرقت دستگیر شود 6/0 است، احتمال اینکه در هشتمین سرقت برای چهارمین بار دستگیر شود چقدر است؟ جواب:
, q =0 4/
⇒ P(X = x) = 8−−1×(0 6/ )4 ×(0 4/ )8 4− = 37 ×0 1296 0 0256/ × /
4 1
×0 1296 0 0256/ × / =0 0193/
مثال: اگر کالایی معیوب باشد مامور کنترل کیفیت با احتمال 8/0 متوجه میشود، احتمال اینکه ششمین کالای معیوب، پنجمین کالایی باشد که وی متوجه میشود، چقدر است؟ جواب:
, p =0 8/ , q =0 2/
pk . qx k− ⇒ P(X = x) = 6−−11×(0 8/ )5 ×(0 2/ )6 5− = 45 ×0 327 0 2/ × /
5
×0 327 0 2/ × / = 5 0 327 0 2× / × / =0 327/
ششم
آمار استنباطی- استاد نصراللهی
مثال: اگر کالایی معیوب باشد احتمال آنکه مشتری بفهمد، 6/0 است، احتمال اینکه پنجمین کالای معیوب،دومین کالایی باشد که مشتری بفهمد چقدر است؟ ضمنا واریانس و امیدریاضی آن را نیز محاسبه کنید.
جواب:
, p =0 6/ , q =0 4/
pk . qx k− ⇒ P(X = x) = 2 15−−1×(0 6/ )2×(0 4/ )5 2− = 14 ×0 36 0 064/ × /
×0 36 0 064/ × / = 4 0 36 0 064× / × / =0 09216/
= 3 33/ V(X) = k.q = 2 0 4× / =1 33/
p 0 6/توزیع هندسی:
اگر در توزیع 2 جملهای منفی 1=k باشد آن را توزیع هندسی میگویند. به طور مثال احتمال اینکه پنجمین فردی که شایعه را شنیده »اولین فردی باشد« بنابراین فرمول این توزیع و امید ریاضی و واریانس عبارتنداز:
1)P(X = x) = p . qx−1 2)E(X) = kp 3)V(X) = pq2
مثال: فردی متقاضی گواهینامه است، با احتمال 65/0 در آزمون رد میشود، احتمال اینکه در دومین آزمون قبول شود، چقدر است؟ جواب:
p =0 65/ , q =0 35/ k =1 x =2
P(X = =x) p . qx−1⇒0 65 0 35/ ×( / )2 1− =0 2275/
مثال: تیراندازی 77/0 از تیرهای خود را به هدف میزند، احتمال اینکه سومین تیر وی اولین تیری باشد که به هدف میخورد چقدر است؟ ضمنا امید ریاضی و واریانس آن را نیز محاسبه کنید .
p =0 77/ , q =0 33/ k =1 x = 3
P(X = x) = p . qx−1⇒0 77/ ×(0 33/ )3 1− =0 77 0 1089/ × / =0 083853/
E(X) = k = 1 =1 29/ V(X) = q = 0 33/ = 0 33/ =0 55/
p 0 77/ p2 (0 77/ )2 0 5929/
توزیع چند جمله ای:
اگر آزمایشی شامل چندین پیشامد باشد و احتمال هر پیشامد در آزمایشهای مختلف ثابت و همچنین آزمایشها مستقل از یکدیگر باشند در این صورت توزیع را توزیع چند جملهای میگویند.
جلسه ششم/ ابوالفضل ولدی/33
مثال: 25/0 از افراد شهری به نامزد اول انتخاباتی،35/0 به دوم و 4/0 به سومی را میدهند،10 نفر هم اکنون پای صندوق رای میباشند، احتمال اینکه 2 نفر به نامزد اول،3 نفر به نامزد دوم و 5 نفر به نامزد دوم رای دهند چقدر است؟ جواب:
P(x1=2,x2 =3,x3 =5)
10 ×( / )2×(0 35 0 4/ ) (3 / )5 =10 9 8 7 6 5× × × × × !×0 0625 0 042 0 0102 0 067/ × / × / = /
0 25
2 3 5, , 2 3 5!× ×! !
ششم
تابع فوق هندسی:
تابع فوق هندسی را به صورت ساده میتوان بیان کرد:
k N −k
x n − x
P(X = x) =
N
n
برای به دست آوردن امید ریاضی و واریانس این توزیع از 2 رابطه زیر استفاده میشود:
nk nk(N −k)(N −n)
E(X) = N , V(X) = N (N2 −1)
مثال: از بین 8 مدیر که به جلسه دعوت شدهاند،3 نفرشان و بقیه وظیفهمدارند، اگر به طور تصادفی 4 نفر انتخاب شوند، احتمال اینکه 2 مدی رابطه مدار باشند چقدر است؟
N = 8 , n = 4 , x = 2 , k = 3
P(X = x) = kx nN−−xk = 23 48−−23 = 2 3!( 3−! 2)! × 2 5( 5−!2)! = 3 10× 30 =0 42/
=
N 8 8! 8× × × ×7 6 5 4! 70
n 4 4 8( −4)! 4× × ×3 2 4!
نکته: به طور کلی اگر N در مقایسه با n (5/0) تفاوت داشته باشد بدین معناست که بین نمونه با جایگزینی و بدون جایگزینی اختلافی وجود ندارد، در این صورت میتوان از توزیع 2 جملهای نیز استفاده کرد.
مثال: از بین 200 متقاضی شغلی تنها 70 نفر واجد شرایط هستند اگر 6 نفر به طور تصادفی انتخاب شود احتمال اینکه 3 نفر از آنها واجد شرایط باشند چقدر است؟ جواب:
چون درصد N بزرگ به n کوچک 35/0 است پس میتوان از توزیع 2 جملهای نیز استفاده کرد.
را هحل اول »توزیع 2 جملهای«:
x = 3 , p =0 35/ , q =0 65/
n px . qn x− ⇒ 6 ×(0 35/ )3 ×(0 65/ )6 3− = 6! ×(0 35/ )3 ×(0 65/ )3
x 3 3 6!( −3)!
3!×(0 35/ )3 ×(0 65/ )3 = 20 0 042875 0 274625× / × / = 2 354/
را هحل دوم: »توزیع فوق هندسی«
هفتم
آمار استنباطی- استاد نصراللهی
N = 200 , k = 70 , n = 6 , x = 3
k N −k 70 200−70
x n P(X = x) =
− x = 3 6−3 = 54 740 357 760/ × / = 19 583 782 400/ / / =0 23764/
N 200 82 408 626 300/ / / 82 408 626 300/ / /
n 6
70 70! = 70 69 68× × ×67! = 54/ 740
=
3 3 70!( −3)! 3× ×2 67!
2006−−370 = 1303 = 3 130( 130−!3)! = 130 129 128 127×3× ×2 127× ×! ! = 357 760/
200 = 200! = 200 199 198 197 196 195× × × × × !×194! = 82 408 626 300/ / /
6 6 200!( −6)! 6× × × × ×5 4 3 2 194!
توزیع پواسون:
در توزیع دو جملهای وقتی n خیلی بزرگ باشد محاسبات بسیار مشکل و پیچیده میباشد. در چنین حالاتی معمولا از توزیع پواسون استفاده کرد و این حالت زمانی است که ∞→n بطور خلاصه میتوان رابطه زیر را بیان نمود.
e−λ.λx
P(X = x) = e = 2 78/ λ = np
xiنکته: در توزیع پواسون میانگین و واریانس برابرند و همانند λ م یباشند. σ = λ
مثال: احتمال اینکه از بین 2000 واحد کالای موجود شرکتی که هر کدام با احتمال 0015/0 معیوباند،5 عدد آنها معیوب باشد چقدر است؟
λ=2000 0 015 3× / =
P(X = x) = e−λ.λx = 2 718/ − ×3 20 07/ ×243 = 2 42/
xi 5 5
مثال: مدیر فروشگاهی احتمال موفقیت فروش که به مشتری به تصادف انتخاب میشود را 3/0 م یداند، اگر
5 مشتری وارد فروشگاه شوند، احتمال اینکه دقیقا3 فروش انجام شود چقدر است؟ جواب:
n = 5 , x = 3 , p =0 3/ , q =0 7/
P(X = x) = n px . qn x− ⇒ P(X = x) = 5 ×(0 3/ )3 ×(0 7/ )5 3−
x 3
⇒ 5! ×0 027 0 49/ × / = 5× ×4 3!×0 027 0 49/ × / =10 0 027 0 49× / × / =0 1323/
3 5!( −3)! 2×3!
مثال: 5/0 کارکنان موسسهای از ساعت کار جدید ناراضیاند، اگر 4 نفر از کارکنان به تصادف انتخاب شوند احتمال آنکه 2 نفر آنها ناراضی باشند چقدر است؟
جلسه هفتم/ ابوالفضل ولدی/37
x 3 3 5
f(x) 0/16 0/34 0/5
P(X=x) 0/16 0/5 1
, p =0 5/ , q =0 5/
n px . qn x− ⇒ P(X = x) = 4 ×(0 5/ )2×(0 5/ )4 2−
x 2
×0 25 0 25/ × / = 4× ×3 2!×0 25 0 25/ × / = 6 0 25 0 25× / × / =0 375/
2 2× !
P(X ≤ 3) =0 5/
مثال: تابع توزیع توام چنین است؟ محاسبه کنید:
z = x + y (ج P(x > y) (ب P(X =1) (الف
مثال: احتمال اینکه نوازدی پس به دنیا آمده 25/0 است، احتمال اینکه سومین فرزند خانواده اولین فرزند پسر باشد، چقدر است؟
x = 3 , k =1 , p =0 25/ , q =0 75/
P(X = x) = p . qx−1⇒ (0 25/ )×(0 75/ )3 1− =0 25 0 5625 0 140/ × / = /
هفتم
توابع احتمال پیوسته:
مشتق:
قانون 1:
مشتق عدد ثابت صفر است.
اگر k یک عدد ثابت باشد.
y = k = y′ =0 :2 قانون
مشتق عدد x یک میباشد.
y = x ⇒ y′ =1 :3 قانون
هر عدد توان دار را به پشت x آورده و یک واحد از توان کم کرده و نوشته:
y = xn ⇒ y′ = xn−1
y = kx ⇒ y′ = knxn−1
مثال:
y = x ⇒ y′ = 7x6
3
y = (2x2 +1)7 ⇒ y′ = 7 2( x2 +1)6 ×4x
1
نکته: مشتق m x = xm م یشود .
مثال: عبارات زیر را به صورت مشتق بنویسید.
11 4 9 1
11y = (x − 1 + x3 x) 2 ⇒ y′ =11(x − x−1+ x )3 2 ×(1− −( 1)+ 4 x )3
x 3قانون 4:
مثال:
y = ex2 = y′ = ex2 ×2x
قانون :5
y = sinu ⇒ y′ = cosu×u′ y = cosu ⇒ y′ = −sinu×u′ y = tanu ⇒ y′ = (1+ tan u)2 ×u′ y = cotu ⇒ y′ = −(1+cot u)2 ×u′
مثال: حاصل عبارات زیر را به صورت مشتق بنویسید.
− 1
y = 2sin x ⇒ y′ = 2×cos x ×( x 2)
1 1
y = etanx ⇒ y′ = etnax ×(1+ tan 1)(−x−2) x ) = (tan x−1) = (1+ tan x2 −1)× −( x−2)
y =1×sin (x )5 4 y′ = 5sin (x )4 4 ×cosx4 ×(4x3) :6 قانون
y = lnu = y′ = u′
u
y = ln(x −sin(x ))2 ⇒ y′ = 1 −cosx2×2x x −sin(x )2 :7 قانون
y = u.vw ⇒ y′ = u vw′ + v uw′ + w uv′
مثال:
y = x sin x2 ⇒ y′ = 2x×sin x + x2 ×cosx
y = x e2 −x tan x y′ = 2x×e−x ×tan x +e−x × −( 1)×x2×tan x +(1+ tan x)2 ×x2×e−x
قانون شماره 8:
y = uv ⇒ y′ = u v′ u−2v u′
مثال:
1 xsin x −ln(1×sin x −cosx)
⇒ y′ = x
(xsin x)2 :انتگرال
همان بدست آوردن تابع اولیه میباشد در صورتی که حد پایین و بالای انتگرال نداشته باشیم به آن انتگرال نامعین میگوییم.
∫f(x)dx
مثال: تابع اولیه 2f(x) = 3x را بیابید.
∫3x dx2 = x3 +c
دستورهای انتگرال گیری:
∫ 1 = ln x +c 2) dx x
4)∫cosxdx = sin x +c
6)∫csc xdx2 = −cot x +c
1)∫ x dxn = xn+1 +c n +1
3)∫sin xdx = −cosx +c
5)∫sec xdx2 = tg x +c
7)tgxdx = −ln cosx +c = ln secx +c
8)cotgxdx = ln sin x +c
9)secx.tgxdx = secx +c
10)cscx.cotgdx = −cscx +c
1
+c
مثال: انتگرالهای نامعین زیر را حل کنید.
1) (∫ 3x2 −4x +2)dx =
1 5
dx = ∫x2 xdx −3∫ 1 dx = ∫ x x2 2 −3∫ 1 = ∫ x2 −3∫ 1 dx
4− x2 4− x2 4− x2
−3sin−1( )x +c 2
∫ 2 +2∫xdx −3∫dx +4∫ 1 dx −5∫ 1 dx = x3 + 2x2 −3x +4ln x −5 x−1 +c x dx x x2 3 x −1
4)∫2x −5sin x + 4 2dx = ∫2xdx −5∫sin xdx +4∫ 3 +1x2
3 + x
⇒ . cosx ( ) tg ( ) c
dx = ∫ x2 +4x +4 = x2 +4x +4dx = ∫x dx53 +4∫ x dx32 +4∫x dx
1 1 x3 x3
2+1 − +1 1
x3 x 3
( ) ( ) c
متغیر تصادفی پیوسته:
در فصل پیش درباره متغیر تصادفی گسسته و توابع احتمال آن بحث شد. در این فصل درباره متغیرهای تصادفی پیوسته و چند نوع توابع مهم آن بحث خواهیم کرد.
فرض کنید میخواهیم احتمال روی دادن تصادف در یک اتوبان 40 کیلومتری مشخص کنیم. همچنین فرض نمایید احتمال وقوع تصادف در هر نقطه از این اتوبان برابر باشد. در این صورت فضای نمونه این آزمایش پیوست دارد. از نقاطی است روی 0تا 40 کیلومتر واقع شده است.
x
بنابراین احتمال اینکه در هر فاصلهای به اندازه x تصادفی رخ دهد برابر است با: =P
40
مثال احتمال اینکه تصادف در جایی بین کیلومتر 10 و 40 اتفاق افتاد برابر است با: 30 = −40 10 =P
40 40مثلا احتمال اینکه تصادف در فاصله کوچکی یک سانتیمتری روی دهد برابر است با:
P =
بنابراین وقتی فاصله به صفر گرایش پیدا میکند احتمال وقوع تصادف در آن فاصله نیز به صفر میل میکند. این بدان مفهوم نمیباشد که امکان پیشامد تصادف وجود ندارد بلکه چون طول فاصله بی نهایت کوچک میشود م یتوان چنین فرض کرد که احتمال وقوع تصادف در یک نقطه مشخص تقریبا صفر است.
تابع احتمال چگالی:
تابعی که معرف متغیر تصادفی پیوسته باشد را تابع چگالی احتمال میگویند که این احتمال در این الت برابر است با مساحت زیر منحنی تقریبا توزیع نرمال و برابر با »یک« م یباشد.
تابع احتمال چگالی را با نماد f(x) نشان میدهند.
احتمال اینکه متغیر تصادفی پیوسته »x« مقداری بین 2 نقطه a وb را بگیرد برابر است با رابطه زیر:
∫
b
P(a ≤ x ≤ b) =f(x)dx
a
توجه شود همانطور که قبلا بیان گردید در متغیرهای تصادفی پیوسته احتمال اینکه متغیر تصادفی »x« دقیقا
∫
a
یک مقدار مشخص بگیرد برابر با صفر است: 0=P(a ≤ x ≤ a) =f(x)dx
a
همچنین توجه داشته باشید که نکات زیر در توابع احتمالی پیوسته رعایت شود:
1- احتمالات همیشه غیر منفی است.
∫
b
2- سطح زیر منحنی یا انتگرال را برابر با »یک« فرض میکنیم. 1=P(X = x)f(x)dx
a
بنابراین تابعی با مقادیر f(x) را که در مجموعه اعداد حقیقی تعریف شده باشد تابع احتمال چگالی گفته میشود و چنین بیان میکنیم:
1)f(x) ≥0
1=2)f(x)dx مثال: متغیر تصادفی x با تابع چگالی زیر مفروض است محاسبه کنید، موارد زیر را:
x 1 < x < 2
− k ,0
f(x) = 16
0 o.w
الف) مقدار k چقدر است.
P( /0 5 ≤ x ≤1 5/ ) (ب P(1≤ x ≤ 3) (ج :«جواب قسمت »الف
∫2 1 =1⇒x2 − 1 kx2 = ( )2 2 − 1 k( )2 − ( )0 0 − 1 k( )0
(x − k)dx
0 16 2 16 0 2 16 2 16
= 2− 216k −[ ]0 = 3216−2k =1⇒ −2k =16−32⇒ −2k = −16 ⇒ k = −−162 = 8
جواب قسمت »ب«:
x − 1 k ⇒ x − 1 ( )8 ⇒ x − 8 ⇒ x − 1
16 16 16 2
∫1 5/ (x − 1)dx = x2 − 1 x1 5/ = (1 5/ )2 − 1(1 5/ ) − (0 5/ )2 − 1(0 5/ ) =0 375/ − −( 0 125/ ) =0 5/
0 5/ 2 2 2 0 5/ 2 2 2 2
جواب قسمت »ج :«
دلیل استفاده عدد 2 در کران بالا به این خاطر میباشد که متغیر x تا فاصله بین 0 و 2 را در نظر گرفته و 3 را شامل نمیشود، یعنی P(1≤ x ≤ 3) → P(1≤ x ≤ 2)
∫2(x − 1)dx ⇒x2 − 1 x2 =1
1 2 2 2 1
مثال: در یک شرکت مواد غذایی میزان ربعی که در قوطیهای 330 گرمی ریخته میشود دارای تابع چگالی زیر است؟
1 x 324 < x < 336
12
0 o.w
آمار استنباطی- استاد نصراللهی
فرض کنید یک قوطی به طور تصادفی انتخاب شود
الف) حداکثر 332 گرم ربع داشته باشد. ب) حداقل 325 گرم ربع داشته باشد.
ج) بین 5/330 تا 5/335 گرم ربع داشته باشد. د) دقیقا 21/330 گرم ربع داشته باشد.
جواب قسمت »الف«
∫332 1 xdx = x2332 = (332)2 − (324)2 = 4 593, −4 374, = 219
324 12 24 324 24 24
جواب قسمت »ب«:
xdx = x2336 = (336)2 − (325)2 = 4 704, −4 402, = 302
24 325 24 24
جواب قسمت »ج«:
1 xdx = x2335 3/ = (335 5/ )2 − (330 5/ )2 = 4 691, −4 552, =139
12 24 330 5/ 24 24
جواب قسمت »د :«
احتمال برابر با صفر است، زیرا دقیقا 21/330 گرم ربع دارد.
مثال: متغیر تصادفی »x« باتابع چگالی زیر مفروض است، محاسبه کنید:
− f(x) = 2e 2x x >0
0 o.w
1) احتمال P(1≤ x ≤ 5) 2) احتمال P(−5 ≤ x ≤ 2 75/ جواب قسمت »الف«:
e−2xdx = 2e−−2x 5 = − e−2x 15 = − e2 5( ) − −e−21( ) = −10e + e2 = − 8e = 2 718/8 =0 339/
2 1
جواب قسمت »ب«:
−
∫02 75/ 2 −2xdx = 2e−2x 02 75/ = − e−2x 02 75/ = − e2 2 75( / ) − −e−20( ) = e−5 5/ +1
e
2
توزیع یکنواخت:
یکی از سادهترین و در عین حال مهمترین توزیعهاتوزیع احتمال یکنواخت است، چنانچه متغیر تصادفی پیوسته »x« را در نظر بگیریم که مقایدر این توزیع بین 2 نقطه α و β انتخاب شود را با شرط اینکه α < β توزیع احتمال یکنواخت میگویند. به طور کلی رابطه این توزیع را میتوان به صورت زیر بیان کرد:
1 α < x < β
f(x) = β−α
0 o.w
امید ریاضی و واریانس توزیع یکنواخت:
برای به دست آوردن امیدریاضی و واریانس این توزیع باید از انتگرالگیری استفاده کرد، در حالتهای خاص نیاز به انتگرالگیریهای جزءبهجزء میباشد در اینجا صرفا به فرمول آن اشاره میکنیم.
E(X) = 1(β+α) V(X) = 1 (β−α)2
2 12
مثال: سود شرکتی دارای توزیع یکنواخت بین 3- و 5 است، موارد زیر را محاسبه کنید.
1) تابع آن را بنویسید
2) احتمال آنکه سود شرکت بین 0 و 5/3 باشد
3) متوسط سود مورد انتظار چقدر است؟
4) واریانس سود شرکت چقدر است؟
جواب قسمت »الف«
1
α < x < β 1 = 1
−3 < x < 5
β−α ⇒ f(x) = 5− −( 3) 8
0 o.w 0 o.w
جواب قسمت »ب«:
dx = 18 x03 5/ = 3 58/ − 08 =0 43/
جواب قسمت »ج«:
(β+α) ⇒ E(X) = 1(5−3) = 2 =1
2 2 2
جواب قسمت »د :«
V(X) = 1 (β−α)2 = 1 (5+3)2 = 64 = 16
12 12 12 3
مثال: تابع چگالی زیر مفروض است:
1 x 0< x < 5
5
0 o.w
آمار استنباطی- استاد نصراللهی
محاسبه کنید:
1) گشتاور مرتبه اول 2) گشتاور مرتبه دوم جواب قسمت »الف«:
xdx = x25 = 52 −02 = 2 5/
10 0 10 10
جواب قسمت »ب«:
x dx2 = x35 = 53 −03 = 4 17/
30 0 30 30
مثال: توزیع یکنواخت زیر مفروض است، اگر 10α = − و 2 =E(X) باشد، این مقادیر را پیدا کنید.
الف) مقدار β؟ ب) V(X)
ج) احتمال اینکه متغیر تصادفی بین 4 و 5- باشد. د) احتمال اینکه متغیر تصادفی مقداری بزرگتر از 5- باشد؟
جواب قسمت »الف«:
جواب قسمت »ب«:
V(X) = (β−α =) 1 (14+10) = 24 = 2
12 12 12
جواب قسمت »ج«:
1 α < x < β 1 = 1 −5 < x < 4
β−α ⇒ f(x) = 14− −( 10) 24
0 o.w 0 o.w
dx
= 241 x04 = 244 − 240 =0 16/
جواب قسمت »د :«
dx
مثال: سود شرکتی دارای توزیع یکنواخت بین 2 و 4 م یباشد، موارد زیر را حساب کنید.
الف) تابع چگالی آن را بنویسید.
ب) متوسط سود چقدر است؟ ج) واریانس سود شرکت چقدر است؟ جواب قسمت »الف«:
1 α < x < β ⇒ f(x) = 4−1 2 = 12 2 < x < 3
f(x) = β−α
0 o.w 0 o.w :«جواب قسمت »ب
جواب قسمت »ج«:
E(X) = 1(β+α =) 1(4+2) = 6 = 3
2 2 2
جواب قسمت »د :«
جلسه نهم/ ابوالفضل ولدی/51
مثال: اگر تابع چگالی متغیر تصادفی x مفروض باشد:
6(x)(1− x) 0< x <1
f(x) =
0 o.w
الف) احتمال اینکه P(x ) باشد.
ب) احتمال اینکه P(x ) باشد.
ج) P( x )
جواب قسمت »الف«:
1
6(x)(1− x)dx = ∫16x −6x dx2 = 6x2 − 6x31 = 61( )2 − 61( )3 − 6( )31 2 − 6( )31 3
3 2 3 1 2 3 2 3
3
جواب قسمت »ب«:
احتمال برابر با صفر است، زیرا =x م یباشد.
جواب قسمت »ج«:
1 1
(x)( − x)dx = x − x dx2 = 6x2 − 6x32 = 6( )2 2 − 6( )21 3 − 6( )13 2 − 6( )31 3
3 3 2 3 1 2 3 2 3
3
توزیع نمایی:
اگر تعداد موفقیتها یا ورودیها دارای توزیع پواسون باشند، زمان بین موفقیتها یا ورودیها متوالی دارای توزیع نمایی است که معمولا در این بحث به آن توزیع نمایی منفی میگویند.
همانطور که میدانیم زمان پیوسته است، بنابراین این توزیع نیز دارای توزیع پیوستهای است، به طور خلاصه م یتوان تابع چگالی آن را به صورت زیر بیان کرد.
= λe−λx x >0
f(x)
0 o.w
λپارامتر توزیع است و بیانگر متوسط (میانگین) تعداد موفقیت یا ورودیها در واحد زمان است. برای محاسبه کردن احتمالات این توزیع از فرمولهای زیر میتوان استفاده کرد:
P(X x) e−λx e−λx e−λx
همچنین احتمال اینکه زمان بین 2 موفقیت یا ورودی بیش از »x« طول بکشد، رابطه زیر صادق است:
P(X > x) = −1 f(x) = e−λx
میانگین و واریانس این توزیع عبارت است از:
E(X) = λ1 V(X) = λ12
توزیع گاما:
تابع متغیر تصادفی پیوستهای است که چگالی آن با تابع آن به شرح زیر میباشد:
a
E(X) = β a
V(X) = β2
2β = باشد موارد زیر را محاسبه کنید , مثال: چنانچه 1a =
− x
f(x) = β ×a1 a ×xa−1×e β x >0
0 o.wدر این تابع 0>a و 0β > و اگر a یک عدد صحیح باشد آنگاه میتوان نوشت:
R(a) = (a −1)!
امید ریاضی و واریانس این توزیع به شرح زیر است:
الف) توزیع آن را بنویسید.
ب) امید ریاضی و واریانس را آن چقدر است؟ جواب قسمت »الف«:
−
x x >0⇒ f(x) = 2 1 ×x1 1− ×e−2x = 1×e−x2 x >0⇒ f(x) = 1e−x2 x >0
f(x) = ×xa−1×e β 1×1 2 2
0 o.w 0 o.w 0 o.w
جواب قسمت »ب«:
a 1 =0 5/ E(X) = = β 2
a 1 = 1
= =V(X) 4 22 2βتوزیع نرمال:
مهمترین توزیع پیوسته است، توزیع نرمال توزیع زنگوله شکلی است که به عبارتی این توزیع بیان میکند که هر یک از پدیدههای واقعی باید دارای تقارن نسبت به خط وسط زنگونه باشد هرگونه جمع آوری دادهها و بررسی آنها مورد شک و تردید است (نظر فرانسیس) م یباشد ولی با گذشت زمان کم کم این عقیده زیر سوال رفت. به هر حال اهمیت این توزیع در موارد زیر است:
الف) بسیاری از پدیدههای طبیعی دارای این توزیع میباشند( عدم دخالت انسان)
ب) در بسیاری از تحقیقات در حوزههای مختلف بسیاری از آنها تقریبا دارای این توزیع یا متمایل به آن م یباشند.
این توزیع چنان تعریف میشود:
متغیر تصادفی پیوسته x با میانگین (امید ریاضی) صفر و انحراف معیار 1 را توزیع نرمال گویند و با استفاده از رابطه زیر میتوان آن را محاسبه کرد.
f(x) = 2 πσ1 2 ×e−12 ×x σ−µ2
X ~ N( , )0 1 π = 3 14135/
e = 2 71828/خصوصیات توزیع نرمال:
خصوصیات این توزیع را به طور خلاصه بیان میکنیم:
1) سطح زیر منحنی بالای محور Xها برابر با »1« است، یعنی:
f(x) = f(x)dx =1
2) به ازای تمام مقادیر »x« همیشه مقدار f(x) بزرگتر یا مساوی صفر است. 0≥f(x)
3) حداکثر مقدار تابع در x = M همیشه برابر است با: 0= ′′f (x)′ =0 , f (x) و الی آخر.
4) تابع حول میانیگن متقارن است، در این حالت خواهیم داشت:
f(x −µ) = f(x +µ)
5) امید ریاضی و واریانس »x« به ترتیب همان µ و 2σ است.
µ = E(X) = x×f(x)dx
6) با دور شدن از میانگین به سمت چپ یا راست منحنی به محور »x«ها نزدیک و نزدیکتر میشود. ولی هی چگاه آن را قطع نمیکند به بیان ریاضی خواهیم داشت:
lim f(X) =0 , lim f(x) =0
x→−∞ x→+∞
7) در این توزیع همیشه میانگین مساوی با میانه مساوی مد میباشد.
µ = md = MO
8) احتمال فاصلهای به اندازه یک انحراف معیار در هر یک از دو طرف میانگین برابر 683/0 و همچنین به اندازه دو انحراف معیار برابر با 954/0 (در دو طرف) و نهایت با سه انحراف معیار در دو طرف برابر با 9998/0 است.
9) همانطوری که گفته شد در این توزیع امید ریاضی صفر و واریانس آن یک است.
E(X) =0 , V(X) =1
با توجه به خواص گفته شده با داشتن میانگین و واریانس هر متغیری (در صورتی که نرمال باشد)، باید ابتدا آن را به توزیع نرمال استاندارد تبدیل کرد و سپس به راحتی کار از جداولی که در این خصوص برای توزیع نرمال تهیه شده است استفاده میکنیم. به دین منظور با تبدیل متغیر تصادفی x به z مقیاس تغییر کرده و میتوان مسائل را حل کرد.
بدین منظور به روابط زیر توجه شود:
x −µ
z = σ
f(x) = µ =0
σ =1
توزیع نرمال با میانگین 30 و انحراف معیار 9 در دست است، احتمال اینکه متغیر تصادفی »x« مقداری بین 24 و 34 بگیرد چقدر است.
x −µ
ج) دایره کنترل کیفیت میزان آبلیموی 70 شیشه را به صورت تصادفی وزن میکند انتظار میرود چند شیشه بیش از 335 گرم آبلیمو داشته باشد.
جواب قسمت »الف«
322−330 ≤ x ≤ 328−5 330 = −( 1 6/ ≤ x ≤ −0 4/ )
5
/0 2034=جواب قسمت »ب«:
=1⇒ P = =1 0 8413/
جواب قسمت »ج«:
یازدهم/ ابوالفضل ولدی/58
احتمالات الف) P(z ≤1 25/ ) ب) P(z ≤ −0 4/ ) ج) P(z ≥1 59/ ) جواب قسمت »الف«:
با استفاده از جدول توزیع نرمالP =0 8944/ جواب قسمت »ب«:
با استفاده از جدول توزیع نرمال P =0 3446/ جواب قسمت »ج«:
P =[z ≥1 59/ ] = −1 [z ≥1 59/ ] = −1 0 9441/ =0 559/
مثال: یک توزیعی دارای 50µ = و 20σ = دقیقهای میباشد، هزینه هر بار تعمیر کردن 5,000 ریال است،اگر تعمیر این ماشین بیش از 85 دقیقه طول بکشد به علت توقف خط تولید ضرری برابر با 1,000 ریال به بار م یآید. E(X) این توزیع چقدر است؟ جواب:
1 75/ ⇒ P =0 9599/
بعد از به دست آوردن عدد 75/1 به جدول مراجعه کرده و احتمال آن را با استفاده از جدول که عدد 9599/0 م یباشد استخراج میکنیم. از طرفی همانطور که میدانیم در صورت مسئله گفته شده است تامین بیش از 58 دقیقه، یعنی:
=0 0401/
× / ×(5 000 100000, + , ) = 4 799 5, / +4 210 5, / = 9 010,
استفاده معکوس از توزیع نرمال:
همانطور که گفته شد در استفاده مستقیم از توزیع نرمال، ابتدا »z« را مشخص و سپس احتمال آن را از جدول پیدا کرده امادر استفاده معکوس مقدار »z« برای ما مشخص نیست ولی احتمال آن معلوم است، بر این اساس احتمال را از جدول پیدا کرده و »z« متناظر با آن را مشخص میکنیم که از رابطه زیر به دست میآید.
x = µ +σz مثال: چنانچه 64 2σ = و دادهها به ترتیب 5،5،4،2 باشد و مقدار متغیر تصادفی 8 باشد، مقدار توزیع نرمال چقدر است؟
جواب:
σ =2 8 µ = 2+4+5+5 = 16 = 4
4 4
z = x −µ = 8−4 = 4 = 1 =0 5/ =0 6915/
σ 8 8 2
جلسه یازدهم/ ابوالفضل ولدی/59
اگر مقدار 12σ=2 µ=4 z = باشد مقدار احتمال توزیع نرمال چقدر است؟ جواب:
28 = ×2 12+4 =x = µ +σz ⇒ x مثال: میزان مصرف مواد اولیه ماهانه در یک شرکت تولیدی دارای توزیع نرمال با میانگین 752µ = و 86σ = است، این شرکت مواد اولیه مورد نیاز خود را تهیه میکند، میخواهیم ثابت کنیم شرکت باید چند تن مواد اولیه برای ماه بعدی سفارش دهد تا با سطح اطمینان 95/0 کمبودی نداشته باشد.
جواب:
با استفاده از جدول 645/1=59/0
x = µ +σz ⇒ x = 752+ 86 1 645( / ) = 893 47/
یازدهم/ ابوالفضل ولدی/60
مدیریت مالی- استاد آشتیانی
رگرسیون:
رگرسیون خطی:
واژه رگرسیون به معنی بازگشت است و نشان دهنده آن است که مقدار یا متغیر، از یک متغیر به متغیر دیگر تغییر میکند، این واژه توسط فرانسیس کالتون مطرح شد. در رگرسیون به دنبال برآورد رابطهای ریاضی بر متغیرها و تحلیل آن است.
به طوری که بتوان مقدار متغیر مجهول را با استفاده از متغیرهای معلوم مشخص کرد
در بررسی رگرسیون نیاز به بحث درباره شیب خط و معادله ان میباشید که از آن صرفنظر شده و فقط به 2 رابطه زیر میپردازیم:
∑xy −nx y
1)a = y −bx b = ∑x2 −n(x)2
و نهایتا رابطه اصلی رگرسیون:
y = a + bx
∑xy−nx y 1082−9 19 78( / ×5 67/ ) = 2 2939/
=
∑x2 −n(x)2 321 9 5 67− ( / )2
a = y −bx =19 78/ −(2 2939 5 67/ × / ) = 6 7735/
جامعه چقدر است؟ MO محاسبه کنید،µ =12 , md =14 مثال: چنانیچه (µ −3 MO) = 3(µ −3 m )d = (12−MO) = 3 12 14( − ) =12−MO = −6 ⇒ MO =18
مثال: چنانچه 160=V(X)، فاصله طبقات باشد محاسبه کنید مقدار تصحیح شپارد چقدر است؟
دوازدهم/ ابوالفضل ولدی/62
مدیریت مالی- استاد آشتیانی
است؟
=0 5/
P(x > y) = P(x =1,y =0)+ P(x = 2,y =0) =0 1 0 2/ + / =0 3/
E(X) = np = 4 0 25× / =1
V(X) = n.pq = 4 0 25× / ×(0 75/ ) =0 75/
هدف این فصل آشناسازی دانشجویان با پارامترهای مرکزی و پراکندگی در جوامع کوچک ( 20≤N ) میباشد.
در فعالیتهای متنوعی از قبیل تجربیات آزمایشگاهی، نظر خواهی از مردم و بررسی سندهای تاریخی با فرآیند جمع آوری دادهها سروکار داریم. فرآیند جمع آوری دادهها هرچه باشد، مجموعه دادههای حاصل معمولاً متشکل از اندازههای عددی است که میتواند از تعدادی محدودی ارقام تا صدها و بلکه هزارها عدد را در بر داشته باشد و در مواجهه با تعداد زیادی از اندازهها ذهن انسان نمیتواند محتوای کلی اطلاعات ثبت شده در مجموعه داده را فوراً درک کند . خلاصه کردن و توضیح خصوصیات مهم مجموعه دادها را معمولاً آمار توصیفی مینامند.
پارامترهای توصیفی که در این فصل مطالعه میشوند را میتوان به صورت زیر بیان کرد.
قبل از بیان شاخصها چند نماد معرفی میکنیم.
مجموعه دادهها متشکل از تعدادی اندازه است که به طور نمادی به صورت 1 , 2x n ,,x x نشان داده میشوند . آخرین زیرنویس (n ) مربوط بهxn ، نشان دهنده تعداد دادههاست، و 1,x 2 ,x به ترتیب نشان دهنده اولین مشاهده، دومین مشاهده، و الی آخر، هستند.
در مطالعه آمار، همه جا با عمل جمع کردن دادهها یا اعداد دیگری که با استفاده از دادهها به دست میآیند، سروکار داریم . برای اجتناب از نوشتن مکرر علامت (+)، نماد (حرف بزرگ یونانی سیگما) را به عنوان اختصار ریاضی برای عمل جمع به کار میبریم.
n
نماد i 1 x i نشان دهنده مجموع n عدد 1 , 2x n ,,x x است این نماد به این صورت خوانده میشود :
مجموع تمام x iها، که i از 1 تا n تغییر میکند.
n
i 1 x i x 1 x 2 x n
جملهای که بعد از نماد نوشته میشود، نشان دهنده مقادیری است که باید جمع شوند، و نمادهای پایین و بالای دامنه زیرنویس i را معین میکنند.
پارامتر مرکزی
به هر معیار عددی که معرف مرکز مجموعه دادهها باشد، پارامتر مرکزی اطلاق میشود یعنی همان مقدار
نمایندهای که مشاهدات در اطراف آن توزیع شده اند. مهمترین پارامترهای مرکزی
1- میـانگین؛ شامـل میانـگین حسـابی، میانگین پیراسـته، میانگین وینزوری، میانگین هندسـی، میانگینهارمـونیـک 2- میانه 3- مد ( نما ) 4- چارکها؛ شامل چارک اول، چارک دوم، چارک سوم
1- میانگین
به نقطه تعادل یا مرکز ثقل توزیع، در دادههایی که بصورت منظم بر روی یک محور ردیف شده باشند، میانگین ( Mean ) اطلاق میشود.
1-1 میانگین حسابی
1-1-1 میانگین حسابی ساده این میانگین از تقسیم مجموع مشاهدات بر تعداد آنها بدست میآید.
n
X i
x i 1N
1-1-2 میانگین حسابی موزون
اگر هر یک از مشاهدات دارای وزنی باشند، و این وزنها را با w i نشان دهیم. در این صورت میانگین حسابی موزون به صورت زیر تعریف میشود.
k
w i W1 k i X i WNi X i
W i
i 1
مثال1: الف) دروس ابتدایی فردی به شرح زیر است، مطلوب است معدل او
در
ی ا
ت
نمره 18 19 2
x 18193 2019
ب) نمرات درس دبیرستان به شرح زیر میباشد، دقت فرمائید که هر درس بر حسب اهمیت خود واحدی نیز دارد :
x 18/88
د ریا ضی ادبیا ت علو
و 4 2 3
ن
18 19 20
م
مثال2: الف) نمره مسئولیت پذیری 5 مدیر عبارت
است از
x i 10 15 14 8 13, , , ,
میانگین نمره مسئولیت پذیری این 5 مدیر را محاسبه کنید.
12x 10 15 145 8 13 605 ب) نمرات مسئولیت پذیری 20 مدیر به صورت زیر است.
x i
(نمره
( 5 6 10 12 15
w i
(تکرا ر) 3 2 5 6 4
/10 45w (3 5) (2 63) 2(5 510)6 (64 12) (4 15) نکته: زمانی که در مشاهدات تکرار وجود دارد. تکرارها به عنوان وزن مشاهده محصوب میشوند.
خواص میانگین حسابی:
1- جمع جبری اختلاف مجموعهای از اعداد از میانگینشان برابر صفر است. یعنی:
N
i 1 (x i x ) 0
2- هر گاه هر یک از مشاهدات با عدد ثابت a جمع شود، و در عدد ثابت b ضرب شود. میانگین اعداد حاصل شده برابر میانگین مجموعه اعداد قبلی ضرب در b به اضافه a خواهد بود. یعنی:
y i b x i a y b x a
3- اگر x و z دو مجموعه از مشاهدات باشند. و مجموعه y از جمع دو به دو اعداد x و z حاصل شده باشد، میانگین مجموعه y برابر استبا جمع دو میانگین مشاهدات x و z. یعنی:
y i x i z i y x z
1-2 میانگین پیراسته
از این میانگین زمانی استفاده میشود که در توزیع مشاهدات، تعداد اندکی از آنها، با بقیه دادهها همخوانی
و تجانس نداشته باشد.
طرز بدست آوردن میانگین پیراسته
1- مرتب کردن صعودی دادهها
2- حذف تمام مشاهدات کوچکتر از LN % پایین و بزرگتر از %LN بالا
3- محاسبه میانگین برای باقیمانده مشاهدات
1-3 میانگین وینزوری
در این میانگین بجای حذف کامل %LNها، مقادیر بالا و پایین آن بجای مقادیر حذف شده مورد استفاده قرار میگیرند و از تعداد دادهها کاسته نمیشود
مثال3: هزینه ماهانه یک خانواده تهرانی به این صورت به دست آمده است:
هزینه بر حسب صد هزار ریال: 5/14, 15, 30, 25, 18, 17, 16, 9, 20, 15, 8, 10 میانگین پیراسته و وینزوری را در صورتی که 25= LN% باشد، محاسبه کنید.
8 9 10 14 5 15 15 16 17 18 20 25 30, , , / , , , , , , , ,
N 12
%LN N 0 25/ 12 3
x 15 91/
x 14 5/ 14 5/ 14 5/ 14 5/ 1512 15 16 17 18 18 18 18 19312 16 08/
1-4 میانگین هندسی
از این میانگین برای محاسبه اندازههای نسبی همانند نسبتها، در صدها، شاخصها و نرخهای رشد
استفاده میشود.
1-4-1 میانگین هندسی ساده
میانگین هندسی یک رشته عدد همانند 1X N،. . . ، X 2 ، X برابر است با ریشه N ام
حاصلضرب آن اعداد
1
G (X X1 2 ... X N )N
1-4-2 میانگین هندسی موزون
اگر دادهها در میانگین هندسی دارای وزن باشند، از این نوع میانگین استفاده میشود.
1
G (X 1w 1 X 2w 2 ... X Kw K )N
مثال4: الف) شاخص قیمت 5 نوع کالای مختلف در سال 1361، عبارت است از:
120، 130، 135، 137، 140 متوسط شاخص قیمت را محاسبه کنید؟
G (120 130 135 137 140) 132 21/
ب) شاخص قیمت 15 نوع کالای مختلف در سال 1361، به صورت زیر است، متوسط شاخص قیمت را محاسبه کنید؟
شاخص قیمت 1 13 1 1 1
تعداد 2 5 3 4 1
G (1202 1305 1353 1374 1401 ) 132 07/
1-5 میانگینهارمونیک
از این نوع، برای محاسبه میانگین مشاهداتی استفاده میشود که از مقیاسهای ترکیبی همانند » کیلو در
ساعت « یا » دور در ثانیه « برخوردار هستند.
1- 5-1 میانگینهارمونیک ساده
این میانگین برای چند اندازه یا مقدار برابر است با عکس میانگین حسابی معکوس آن اندازهها
N N
H N
x x1 2 x N i 1 x i
1-5-2 میانگینهارمونیک موزون
در صورت تکرار دادهها ( وزن داشتن آنها ) از فرمول زیر استفاده میشود :
H w 1 ww2 ...i w k k Nw i
x 1 x 2 x k i 1 x i
مثال5: الف) وسیلهای مسافت تهران – کرج را با سرعت 80 کیلومتر بر ساعت رفته و با 120 کیلومتر بر ساعت برگشته است متوسط سرعت رفت و برگشت فرد چقدر است؟
H 11 2 96km/h
ب) وسیلهای مسافت تهران – قم را این گونه رفته و برگشته :
مسیر رفت را با سرعت km / h80 و باقیمانده را با سرعت km / h100 رفته و کل مسیر برگشت را با سرعت km/ h110طی کرده است مطلوب است متوسط سرعت این وسیله در رفت و برگشت.
W.H 31 23 1 100/ 3km/ h
1 2
3 3 1
80 100 110
2- میانه
مراحل محاسبه میانه
1- مرتب کردن اعداد.
2- تعیین نقطهای که نیمی از دادهها بالاتر و نیمی دیگر پایین تر از آن هستند.
نکته: در صورتی که تعداد دادهها فرد باشد میانه عددی است که در وسط قرار دارد و اما در صورتی که تعداد دادهها زوج باشد، میانه عبارتست از معدل دو نمرهای که در وسط واقع میشوند.
مثال6: میانه مشاهدات زیر را محاسبه کنید.
6 - 4- 9 -13 - 17
4 - 6 - 7 -9 6 5/
3- مد ( نما )
به مقداری گفته میشود که در میان سایر مقادیر توزیع، بیشترین تکرار را داشته باشد، مد را با Mo نشان میدهند. مثال7: مد مشاهدات 2, 2, 5, 15, 10, 8, 5, 2 را بیابید.
Mo 2
نکته: چنانچه کلیه مشاهدات به یک اندازه تکرار شده باشند، جامعه فاقد مد یا مد جامعه تهی خواهد بود.
4- چارک
اگر جامعه آماری به چهار قسمت مساوی تقسیم شود، به هر یک از قسمتها یک چارک گفته میشود و
آنها را با Q نشان میدهند.
انواع چارکها
: 1Q مقداری که 25% مشاهدات، کمتر از آن و 75% بیشتر از آن است.
2Q : مقداری که 50% مشاهدات، کمتر از آن و 50% بیشتر از آن است.
3Q : مقداری که 75% مشاهدات، کمتر از آن و 25% بیشتر از آن است.
نحوه محاسبه چارکها
1- مرتب نمودن صعودی دادهها
2- کد گذاری کردن آنها از 1 تا N
3- پیدا نمودن محل چارک مورد نظر 21CQ a aN4
که در فرمول فوق 1و2و3 a= و تعداد مشاهدات N=
4- تعیین نمودن مقدار چارک مورد نظر به کمک محل چارک مثال 8: چارک اول، دوم و سوم مشاهدات زیر را به دست آورید:
80, 90, 50, 60, 100, 70, 75, 80, 70, 80, 60 حل:
50 ,60 ,60 , 70 ,70 ,75 ,80 ,80 ,80 ,90 ,100
CQ1 1411 21 3 25/ Q1 60 0 25/ (70 60) 62 5/
CQ2 6 Q2 75
CQ3 34 11 21 8 75/ Q3 80 0 75/ (80 80) 80
پارامترهای پراکندگی
شاخصهایی هستند که متوسط میزان دوری و نزدیکی دادههای توزیع را نسبت به میانگین شان نشان میدهند.
انواع شاخصهای پراکندگی
1- دامنه تغییرات 5- انحراف معیار
2- دامنه میان چارکی 6- نیمه واریانس
3- انحراف متوسط از میانگین 7- ضریب پراکندگی
4- واریانس
1- دامنه تغییرات( R )
سادهترین شاخص پراکندگی است و با کم کردن کوچکترین مشاهده از بزرگترین آنها در یک سری توزیع بدست میآید.
R MAX x MIN x
مثال9: کارگاهی دارای 15 کارگر است که حقوق ماهانه آنها(گرد شده به صد هزار تومان ) به قرار زیر است:
12, 11, 19, 16, 22, 8, 13, 16, 17, 15, 20, 14, 17, 14, 15 دامنه تغییرات مشاهدات را به دست آورید.
R 22 8 14
2- دامنه میان چارکی( IQR )
این شاخص، پراکندگی دادهها را در فاصله چارک اول و چارک سوم نشان میدهد و کاری به مقادیر کوچکتر از 1Q و بزرگتر 3Q ندارد.
برای محاسبه این شاخص، کافیست که مقادیر 1Q و 3Q را بدست آورده و از هم کم کنیم.
IQR Q Q3 1 .
مثال 10: در مثال 9 دامنه میان چارکی را محاسبه کنید.
8 ,11 ,12 ,13 ,14 ,14 ,15 ,15 ,16 ,16 ,17 ,17 ,19 ,20 ,22
CQ1 1415 21 4 25/ Q1 13 0 25/ (1413) 13 25/ CQ3 3415 21 11 75/ Q3 17 0 75/ (17 17) 17
Q3 Q1 17 13 25/ 3 75/
3- نیمه میان چارکی (انحراف چارکی)
برای بدست آوردن این شاخص، که به انحراف چارکی نیز معروف است، کافیست، مقدار دامنه میان چارکی را بر عدد 2 تقسیم نماییم.
Q Q3
SIQR 1
2مثال 11: در مثال 9 نیمه میان چارکی را محاسبه کنید.
SIQR Q Q3 2 1 17 13 252 / 1 875/
شاخصهای مناسب برای توزیعهای نا متقارن 1- استفاده از میانه بعنوان بهترین شاخص مرکزی
2- استفاده از انحراف چارکی بعنوان بهترین شاخص پراکندگی
4- انحراف متوسط از میانگین
این شاخـص از تقسیم مجموع قدر مطلـق انحـرافات تک تک مشاهدات از میانگین شان بر تعداد مشاهدات بدست میآید.
n
X i x
A D. i 1
Nمثال 12: در مثال 9 انحراف متوسط از میانگین را محاسبه کنید.
n
A D. i 1 XNi x | 15 15 27/ | | 14 15 27/15 | ..... | 12 15 27/ | 40 2715/ 2 68/
محاسن و معایبAD
محاسن : در نظر گرفتن تغییرات کل دادهها معایب : 1- نشان ندادن تأثیر انحرافات بزرگ
2- بی بهره بودن از بعضی از خواص مطلوب میانگین حسابی
5- واریانس
در این شاخص پراکندگی، بر خلاف شاخص انحراف متوسط از میانگین بجای قدر مطلق از مجذور (توان 2) انحرافات استفاده میشود.
N
(X i x )2
x2 i 1
Nمثال 13: در مثال 9 واریانس مشاهدات را محاسبه کنید.
N
x2 i 1 (XNi x )2 (15 15 27/ )2 (14 15 27/15 )2 .....(12 15 27/ )2 178 9315/ 11 93/
6- انحراف معیار
این شاخص به منظور برطرف کردن عیوب شاخصهای قبلی است یعنی همان نشان ندادن تأثیر انحراف بزرگ توسط AD و افزایش دادن تأثیر این انحراف توسط 2X.
و یا
مثال 13: در مثال 9 انحراف از معیار را محاسبه کنید.
X 2X 11 93/ 3 45/
خواص واریانس
1- اگر تمام مشاهدات با عدد ثابتa جمع شوند، واریانس جدید تغییر نمی کند.
Y i X i a Y2 X2
2- اگر تمام مشاهدات، به عدد ثابت b ضرب شوند، واریانس جدید 2b برابر افزایش مییابد
Y i bX i Y2 b 2X2
7- نیمه واریانس
یعنی متوسط مجذور مقادیر نامطلوب
k
(X i x )2 SV. i 1 k
که N، تعداد کل مشاهدات، K، تعداد موارد نامطلوب و x، میانگین کل مشاهدات میباشد.
مقادیر نامطلوب : در دادههای مربوط به سود و در آمد مقادیر کوچک تر از میانگین و در دادههای مربوط به زیان و هزینه مقادیر بزرگتر از میانگین، نامطلوب قلمداد میشوند.
مثال 14: در مثال 9 نیمه واریانس را محاسبه کنید.
حل: با توجه به اینکه مشاهدات مربوط به درآمد میباشد مقادیر کمتر از میانگین به عنوان مقادیر نامطلوب محسوب شده و نیمه واریانس برابر است با
k
SV. i 1 (Xki x )2 (8 15 27/ )2 (11 15 27/ )2 (12 15 27/ )2 (13 15 278/ )2 (14 15 27/ )2 (15 15 27/ )2 (15 15 27/ )2 90 308/ 11 29/
8- ضریب پراکندگی
ضریب پراکندگی یکی از معیارهای پراکندگی نسبی است که با فرمول زیر بیان میشود
C V XX
که x، انحراف معیار و x، میانگین مشاهدات است.
مثال 15: در مثال 9 ضریب پراکندگی را محاسبه کنید.
C V XX 0 226/
کاربردهای ضریب پراکندگی برای مقایسه دو جامعه در مواردی که :
1- مقیاسها یکسان نیستند
2- مقیاس یکسان ولی تفاوت زیادی در بزرگی مشاهدات وجود دارد
3- واریانسهای جوامع یکسان ولی میانگینهایشان متفاوت است.
هدف این فصل آشنایی دانشجویان با طبقه بندی و سازماندهی مشاهدات و استفاده از نمودارهای مختلف برایتوصیف دادههاست.
توزیع فراوانی
یعنی جدول مرتب و خلاصه شده از دادهها و مشاهدات که تکرار وقوع هر دادهها در آن مشخص شده است.
معمولا یک جدول توزیع فراوانی شامل ستونهای مشخص کننده حد پایین و بالای طبقات( طبقه بندی دادهها)، مرکز دستهها، فراوانی مطلق، فراوانی مطلق نسبی، فراوانی تجمعی، فراوانی نسبی تجمعی است.
1) مراحل طبقه بندی دادهها
1- مرتب کردن دادهها و محاسبه دامنه تغییرات ( R )
2- مشخص کردن تعداد طبقات ( K )
3- محاسبه نمودن فاصله طبقات ( I )
4- سازماندهی طبقات
1- مرتب کردن دادهها و محاسبه دامنه تغییرات یعنی R MAX X i MIN X i
2- فرمولهای محاسبه تعداد طبقات
• فرمول تجربی استورجس K 1 3 32/ LogN
• روش تقریبی N )K N تعداد مشاهدات میباشد )
3- تعیین فاصله طبقات
فاصله طبقات از تقسیم مقدار R (دامنه تغییرات) بر مقدار محـاسبه شـده برای تعـداد طـبقـات (K) به شکلزیر بدست میآید I R
K
4- سازماندهی دادهها
پس از مشخص شدن K و I سازماندهی یعنی تعیین نوع جدول و شیوه طبقه بندی دادهها شروع میشود که این بستگی به نوع دادههای جمع آوری شده دارد.
انواع طبقه بندی دادهها
1- طبقه بندی مشاهدات پیوسته: در این نوع مشاهدات طبقه بندی به دو صورت پیوسته و گسسته انجام میشود.
1. طبقه بندی پیوسته: در این نوع طبقه بندی طول، عرض و فاصله طبقات مساوی هستند. این نوع طبقه بندی برای دادههای اعشاری استفاده میشود.
2. طبقه بندی گسسته : در این نوع طبقه بندی طول و عرض طبقات با هم برابر نیستند. این نوع طبقه بندی برای دادههای غیر اعشاری استفاده میشود.
مهمترین تقریبها در طبقه بندی گسسته
1. تقریب 1/0
2. تقریب 5/0
3. تقریب 1 ( واحد )
تقریب، اختلاف طول و عرض طبقات یا فاصله بین حد بالای یک طبقه با حد پایین طبقه بعدی است.
2- طبقه بندی مشاهدات ناپیوسته
در مشاهدات ناپیوسته تعریف بصورت فاصله طبقات بی معناست لذا برای تشکیل توزیع فراوانی آنها کافیستیک ستون برای مشاهدات و ستون دیگری برای فراوانی آنها تنظیم شود .
2) مرکز دسته ( x i ):
2/ (ابتدای دسته + انتهای دسته)
3) فراوانی مطلق (Fi ): تعداد مشاهدات در هر دسته
4) فراوانی نسبی ( f i ): از تقسیم فراوانی مطلق هر دسته بر تعداد کل مشاهدات حاصل میشود.
f i NF i
کاربرد فراوانی نسبی: به کمک این فراوانی میتوان در صد تراکم دادهها را در هر طبقه مشخص نمود بعبارتی از f i جهت یافتن محل تمرکز دادهها استفاده میشود.
5) فراوانی تجمعی ( FCi )
فـراوانی تجـمعی هر طـبقه، عـبارتست از مجموع فراوانیهای مطلق از اولین طبقه تا طبقه مورد نظر که آن را با FC i نشان میدهند
Fc i F j
j 1
6) فراوانی نسبی تجمعی (fci ) این فراوانی از تقسیم فراوانی تجمعی هر طبقه بر تعداد مشاهدات بدست میآید.
fc i FcN i
مفهوم فراوانی نسبی تجمعی: این فراوانی بیانگر در صد دادهها و مشاهدات واقع شده بین حد پاییناولین طبقه تا حد بالای طبقه مورد نظر است.
مثال 1: ارقام سود روزانه 25 دکه روزنامه فروشی در زیر آمده است. جدول توزیع فراوانی مشاهدات را به دست آورید.
، 78/01، 90/23، 84/92، 56/02، 84/21، 76/73، 77/25، 86/02، 70/88، 64/90، 81/47 ، 55/31
، 66/05، 84/71، 88/64، 76/15، 86/37، 86/51، 74/76، 85/43، 57/41، 87/09، 73/37، 88/05
83/91
حل: ابتدا مشاهدات را طبقه بندی میکنیم. برای این منظور مراحل زیر را انجام میدهیم.
R MAX i MIN i 90 23/ 55 31/ 34 92/ :محاسبه دامنه مشاهدات -1
2- مشخص کردن تعداد طبقات: 5N 25
3- تعیین طول طبقات: 7I Rk 6 984/
4- سازمان دهی مشاهدات: لازم به ذکر است با توجه اعشاری بودن مشاهدات از طبقه بندی پیوسته به منظور طبقه بندی مشاهدات استفاده میشود.
با توجه به سادگی محاسبات، نتایج نهایی در جدول ارائه میشود.
حدود طبقات مرکز دسته (x i ) فراوانی مطلق (Fi ) فراوانی نسبی (f i ) فراوانی تجمعی (FCi ) فروانی نسبی
تجمعی (fci )
[55/3 -62/3) 58/8 3 0/12 3 0/12
[62/3 -69/3) 65/8 2 0/08 5 0/2
[69/3 -76/3) 72/8 5 0/2 10 0/4
[76/3 -83/3) 79/8 3 0/12 13 0/52
[83/3 - 90/3] 86/8 12 0/48 25 1
کل 25 1
مثال2: سن 30 مدیر موسسه در زیر ارائه شده است جدول توزیع فراوانی آنها را به دست آورید.
-46 -48 -47 -57 -44 -45 -59 -42 -43 -55 – 40 -38 -68 – 62 – 50 -54 -69 – 63 – 46 - 35
38 -42- 60 -42 – 60 -59 -36 -49 -64 -43
حل: ابتدا مشاهدات را طبقه بندی میکنیم. برای این منظور مراحل زیر را انجام میدهیم.
R MAX i MIN i 69 36 34 :محاسبه دامنه مشاهدات -1
2- مشخص کردن تعداد طبقات: 6k N 30 5 83/
I Rk 5 67/ 6 :تعیین طول طبقات -3
4- سازمان دهی مشاهدات: لازم به ذکر است با توجه به غیراعشاری بودن مشاهدات از طبقه بندی گسسته به منظور طبقه بندی مشاهدات استفاده میشود.
با توجه به سادگی محاسبات، نتایج نهایی در جدول ارائه میشود.
حدود طبقات مرکز دسته (x i ) فراوانی مطلق
(Fi ) فراوانی نسبی (f i ) فراوانی تجمعی (FCi ) فروانی نسبی
تجمعی (fci )
[35 -41 ] 38 5 0/17 5 0/17
[42 -47 ] 44 10 0/33 15 0/5
[48 -53 ] 50 3 0/1 18 0/6
[54 -59 ] 56 5 0/17 23 0/77
[60 -65 ] 62 5 0/17 28 0/93
[66 -71 ] 68 2 0/067 30 1
کل 30 1
مثال3: در 50 دقیقه متوالی، تعداد تلفنهایی که به یک مرکز تلفن شده است در هریک از دقایق به شرح زیرثبت شده است . جدول توزیع فراوانی را به دست آورید.
-1 -2 -1 -0 -0 -1 -1 -0 -0 -2 -0 -1 -0 -3 -0 -4 -1 -0 -1 -1 -0 -2 -2 -0 -0 -1 -1 – 0 -1
1 -2 -1 -0 -0 -2 -0 -1 -1 -2 -1 -0 -4 -1 -1 -0 -1 -3 -1 -0 -0
حل: با توجه به ناپیوسته بودن مشاهدات از طبقه بندی مربوط به دادههای ناپیوسته به منظور طبقه بندی مشاهدات استفاده میشود.
مشاهدات فراوانی مطلق
(Fi ) فراوانی نسبی (f i ) فراوانی تجمعی (FCi ) فروانی نسبی
تجمعی (fci )
0 19 0/38 19 0/38
1 20 0/4 39 0/78
2 7 0/14 46 0/92
3 2 0/04 48 0/96
4 2 0/04 50 1
کل 50 1
نمایش هندسی مشاهدات
استفاده از نمودارها یا به عبارتی نمایش هندسی مشاهدات در گزارش نویسی باعث میشود که خوانندگان با صرف کمترین زمان و با سادهترین بیان، گزارش را بفهمند و تصویری روشن از توزیع داشته باشند انواع نمودارها
1- نمودارهای کمی : مخصوص دادههایی با مقیاس فاصلهای و نسبی
2- نمودارهای وصفی : مخصوص دادههایی با مقیاس اسمی و یا رتبهای
همانطور که در شکل فوق دیده میشود مهمترین نمودارهای کمی عبارتند از:
1- بافت نگار (هیستوگرام) 4- تحلیل اکتشافی دادهها
2- چند ضلعی (پلی گون) 1-4 نمودار شاخه و برگ
3- فراوانی تجمعی (اجُایو) 2-4 نمودار جعبهای
1-3 پلی گون فراوانی تجمعی
2-3 منحنی فراوانی تجمعی
که در زیر هریک از ننمودارهای فوق تشریح شده است.
1) بافت نگار
بافت نگار نموداریست در دستگاه مختصات که محور افقی آن با حدود واقعی طبقات و محور عمودی آن با فراوانی مطلق یا نسبی درجه بندی میشود.
حدود واقعی: اگر دسته بندی مشاهدات از نوع پیوسته باشد حدود واقعی با حدود طبقات برابر است و در صورتی که طبقه بندی از نوع گسسته باشد برای پیدا کردن حدود واقعی، 5/0 واحد از کران پایین طبقات کم میکنیم و 5/0 واحد به کران بالای طبقات اضافه میکنیم تا دسته بندی مشاهدات پیوسته شود. آنگاه حدود حاصل، حدود واقعی طبقات است.
در صورتی که از فراوانی مطلق به منظور مندرج کردن محور عمودی استفاده کنیم. پس از مدرج کردن محور افقی با استفاده از حدود واقعی (کرانههای هر طبقه) مستطیلی عمودی رسم میشود که ارتفاع آن برابر فراوانی مطلق هر طبقه میباشد.
برای رسم بافت نگار فراوانی نسبی، ردهها (کران پایین و بالای طبقات) را روی محور افقی نمودار مشخص میکنیم . آنگاه روی هر رده، مستطیلی عمودی رسم میکنیم که مساحت آن مساوی با فراوانی نسبی آن رده باشد . در نتیجه ارتفاع مستطیل برابر است با
طول رده / فراوانی نسبی رده = ارتفاع مستطیل
به این ترتیب، مساحت هر یک از مستطیلهای بافت نگار نشان دهنده نسبت مشاهدات موجود در ردهای است که مستطیل بر آن قرار دارد . بنابراین مجموع مساحت تمام مستطیلها در یک بافت نگار برابر با یک است.
برای نمایش فراوانیهای نسبی، استفاده از مساحت مستطیلها به جای ارتفاع آنها فایده آشکاری دارد . به نظر میرسد که در موقع مقایسه کردن دو قسمت یک بافت نگار، یا دو بافت نگار مختلف، چشم انسان به طور غریزی مساحتها را با هم مقایسه میکند.
مثال 4: برای مشاهدات مثال 1 نمودار بافت نگار را رسم کنید.
حل: رسم نمودار بر اساس فراوانی مطلق
برای رسم نمودار فراوانی نسبی، ابتدا فراوانی نسبی هر طبقه را بر طول طبقه که در این مثال 7 است تقسیم میکنیم. بعد از مشخص کردن کران طبقات روی محور افقی روی کران طبقات مستطیلی به ارتفاع مقادیر حاصل از تقسیم رسم میشود.
٣/٩٠ ٣/٨٣ ٣/۶٧ ٣/٩۶ ٣/٢۶ ٣/۵۵ لازم به ذکر از مقادیر داخل هر مستطیل، بیانگر مساحت مستطیلهاست.
مثال 5: برای مشاهدات مثال 2 نمودار بافت نگار را رسم کنید.
حل:
حدود طبقات حدود واقعی طبقات فراوانی مطلق
(Fi ) فراوانی نسبی (f i ) ارتفاع مستطیل
[35 -41 ] 34/5 -41/5 5 0/17 0/028
[42 -47 ] 41/5 -47/5 10 0/33 0/055
[48 -53 ] 47/5 -53/5 3 0/1 0/0167
[54 -59 ] 53/5 -59/5 5 0/17 0/028
[60 -65 ] 59/5 -65/5 5 0/17 0/028
[66 -71 ] 65/5 -71/5 2 0/067 0/011
کل 30 1
٠/١٧
2) نمودار چند ضلعی
نموداریست که متناظر با هر نماینده طبقه ( مرکز طبقه) در محور افقی و فراوانی آن در محور عمودی، یک نقطه در صفحه مختصات ایجادمی شود. به نقاط مزبور دو نقطه فرضی دیگر اضافه میکنیم اولی مرکز طبقه ماقبل اولین طبقه و دیگری نماینده طبقه مابعد آخرین طبقه، از اتصال متوالی نقاط به یکدیگر نمودار مورد نظر حاصل میشود.
مثال 6: برای مشاهدات مثال 2 نمودار چندضلعی را رسم کنید.
3) نمودار فراوانی تجمعی
• پلی گون فراوانی تجمعی
برای ترسیم این نمودار، از نماینده طبقات در محور افقی و فراوانی تجمعی در محور عمودی استفاده میشود، سپس نقاط ایجاد شده به ترتیب به هم وصل میشوند.
مثال 7: برای مشاهدات مثال 2 پلی گون فراوانی تجمعی را رسم کنید.
• منحنی فراوانی تجمعی
تنها فرق این نمودار با نمودار پلی گون فراوانی تجمعی در این است که در این نمودار بجای نماینده طبقات از حد بالای کرانهها استفاده میشود.
مثال 8: برای مشاهدات مثال 2 نمودار فراوانی تجمعی را رسم کنید.
کاربردهای نمودار فراوانی تجمعی
1- برای محاسبه چندکها (چارکها، دهکها، صدکها)
2- برای مقایسه پدیدهها (مثل میزان رشد تورم در کشورها)
4) تحلیل اکتشافی دادهها
در بر گیرنده نمودارهای جدیدی است که در مراحل اولیه تحلیل دادهها مفید هستند و اطلاعات بیشتری را در مورد تک تک دادهها به معرض نمایش میگذارند.
4-1 نمودار شاخه و برگ
برای تهیه این نمودار، ارقام مشاهدات به دو بخش شاخه و برگ تقسیم میشوند، شاخه شامل یک یا چند رقم اولیه و برگ شامل ارقام باقی مانده است.
مثال 9: برای مشاهدات مثال 2 نمودار شاخه و برگ را رسم کنید.
3 5 6 8 8
4 0 2 2 3 3 4 5 6 6 7 8 9
5 0 4 5 7 9 9
6 0 0 2 3 4 8 9
محاسن نمودار شاخه و برگ
در این نمودار بر خلاف بافت نگار، اعداد اصلی از بین نمیروند و محاسبه چندکها هم با استفاده از آن براحتی امکان پذیر است.
4-2 نمودار جعبهای
این نمودار نشان دهنده چارکها و حداقل و حداکثر مشاهدات است و برای مقایسه دو یا چند جامعه آماری مورد استفاده قرار میگیرد.
مراحل تهیه نمودار جعبهای
الف – پیدا کردن حداقل و حداکثر دادهها ب – پیدا کردن چارکهای اول، دوم و سوم
مثال 9: برای مشاهدات زیر نمودار جعبهای را رسم کنید
80, 90, 50, 60, 100, 70, 75, 80, 70, 80, 60 حل:
50 ,60 ,60 , 70 ,70 ,75 ,80 ,80 ,80 ,90 ,100
MIN 50 , MAX 100
CQ1 1411 21 3 25/ Q1 60 0 25/ (70 60) 62 5/
CQ2 6 Q2 75
CQ3 34 11 21 8 75/ Q3 80 0 75/ (80 80) 80
نمودارهای وصفی
این دسته از نمودارها برای نمایش هندسی دادههای کیفی بکار میروند، در این نمودارها هر یک از مقادیر بعنوان یک طبقه در نظر گرفته میشوند.
مهمترین نمودارهای وصفی
1- نمودار ستونی
2- نمودار دایرهای
3- نمودار پاره تو
1) نمودار ستونی (میله ای)
این نمودار در یک دستگاه مختصات که محور افقی نشان دهنده کیفیت مشاهدات و محور عمودیش نشان دهنده فراوانی مطلق یا نسبی هر گروه است ترسیم میشود. در نمودار میله ای، خطوط جایگزین مستطیلها میشوند تا بر این موضوع تاکید شود که فراوانیها واقعا روی فاصله پخش نشده اند.
مثال10: در مدیریت، انسانها را به لحاظ ارتباطات به چهار دسته تصویری، احساسی، صوتی و ارقامی تقسیم میکنند. کارکنان یک سازمان از این لحاظ مورد بررسی قرار گرفتهاند که حاصل تحقیق در این جدول آمده است:
گروه
ارتباطی تصویری احساسی صوتی ارقامی
تعداد
کارکنان 100 150 300 50
2) نمودار دایرهای
این نمودار ابزار مناسبی برای تجسم مشاهدات بوده و معمولاً بر حسب در صد تهیه میشود و به نمودار کلوچهای نیز معروف است مراحل تهیه نمودار دایرهای
1- تبدیل فراوانی مطلق به نسبی
2- پیدا کردن مساحت هر قطاع از دایره با استفاده از رابطه Si 3600 f i
3- تقسیم مساحت دایره بر حسب S iها
4- نوشتن نوع و درصد مشاهدات بر روی دایره مثال11: نمودار دایرهای مشاهدات مثال 10 را رسم کنید.
گروه
ارتباطی تصویری احساسی صوتی ارقامی
تعداد
کارکنان 100 150 300 50
فراوانی نسبی 0/1667 0/25 0/5 0/083
S i 60 90 180 30
3) نمودار پاره تو نحوه رسم نمودار
1- مرتب کردن موضوعات بر اساس فراوانی مطلق آنها به صورت نزولی ( مورد اول دارای بیشترین فراوانی و مورد آخر دارای کمترین فراوانی است.) 2- مشخص کردن موارد روی نمودار افقی
3- مشخص کردن فراوانی مطلق موارد روی نمودار عمودی با استفاده از نمودار ستونی، برای رسم نمودار، ستونها به شکل مستطیل در نظر گرفته میشوند.
4- مشخص کردن درصد فراوانی نسبی تجمعی موارد روی محور سوم (روبروی محور عمودی) با استفاده از نمودار فراوانی تجمعی
مثال11: نمودار پاره تو مشاهدات مثال 10 را رسم کنید.
گروه ارتباطی صوتی احساسی تصویری ارقامی
تعداد کارکنان 300 150 100 50
فراوانی تجمعی 300 450 550 600
درصد فراوانی نسبی تجمعی 50 75 91/67 100
مفهوم نزولی بودن نمودار پاره تو
یعنی این که در این نمودار پر وقوعترین موضوعات در سمت چپ نمودار قرار گرفته، سپس موضوعات با فراوانی کمتر در سمت راست آنها قرار میگیرند.
کاربرد نمودار پاره تو
1- در تحلیل موجودیهای جنسی انبارها
2- در بررسی نواقص سیستمها
3- در بررسی نحوه توزیع درآمد و توزیع پرسنل مؤسسه
هدف اصلی این فصل آشنا ساختن دانشجویان با پارامترهای مرکزی، پراکندگی و تعیین انحراف از قرینگی و کشیدگی در دادههای طبقه بندی شده میباشد سؤالاتی که توزیع فراوانی به آنها پاسخ میدهد.
1- مرکز توزیع کجاست ؟
2- پراکندگی آن چقدر است ؟
3- تمایل داده به کدام سمت است ؟
4- پراکندگی توزیع در مقایسه با توزیعهای مشابه چگونه است ؟
سؤال اول به کمک پارامترهای مرکزی قابل پاسخگویی است به سؤال دوم نیز با محاسبة پارامترهای پراکندگی جواب داده میشود ولی برای پارامترهای مرکزی و پراکندگی فرمولهای جدیدی بر اساس مشاهدات طبقه بندی شده ارائه میشود. برای پاسخ گویی به سوال سوم از پارامترهایی با عنوان »پارامترهای تعیین انحراف از قرینگی« استفاده میشود و به سؤال چهارم با محاسبة شاخص کشیدگی جواب داده میشود.
انواع پارامترهای مرکزی در دادههای طبقه بندی شده
1- میانگین ؛ که به روشهای مستقیم و غیرمستقیم قابل محاسبه است. 2- مد ؛ که نشان دهنده بیشترین تکرار میباشد.
3- چندکها ؛ شامل چارکها، دهکها و صدکها است.
1- میانگین
1-1 میانگین به روش مستقیم
این فرمول برای دادههای طبقه بندی شده به شرح ذیل است :
x FNi X i
که در آن F i، فراوانی مطلق، X i، متوسط طبقات و N، تعداد کل مشاهدات است.
1-2 میانگین به روش غیرمستقیم ( کد گذاری )
x A (NF id i )I
که A، عدد دلخـواه، d i، کد هر طـبقه و I فاصله طبقات است.
در مقدار A میتوان گفت، این عدد بعنوان میانگین تقریبی، از وسط ستون نماینده طبقات انتخاب شده و موجب تسهیل عملیات ریاضی در پیدا کردن میانگین تقریباً واقعی میشود. در موردdi که کد هر طبقه است، به شکل زیر قابل محاسبه میباشد.
d i X Ii A موارد استفاده از فرمول میانگین به روش کد گذاری زمانی است که مشاهدات حالت اعشار داشته یا این که به گونهای تعریف شوند که محاسبه میانگین به روش مستقیم وقت گیر و مشکل آفرین باشد. ستونهای جدول توزیع فراوانی برای روش غیر مستقیم میانگین این ستونها ضروری هستند : 1- حدود طبقات 4- حاصلضرب فراوانی در نماینده طبقه
2- فراوانی مطلق 5- کد طبقات
3- نماینده طبقات 6- حاصلضرب فراوانی در کد طبقه
نکته: از علامت (تقریباً مساوی) در فرمولهای میانگین بدین جهت استفاده میشود که پارامترها به واسطه طبقه بندی مشاهدات (استفاده از نماینده طبقات) دقیق نمیباشند.
مثال 1:جدول توزیع فراوانی ارقام سود روزانه 25 دکه روزنامه فروشی در زیر آمده است. میانگین مشاهدات را حساب کنید.
حدود طبقات فراوانی مطلق (Fi )
[55/3 -62/3) 3
[62/3 -69/3) 2
[69/3 -76/3) 5
[76/3 -83/3) 3
[83/3 - 90/3] 12
کل 25
حل:
حدود طبقات فراوانی مطلق (Fi ) مرکز دسته (x i ) F xi i کد طبقه (di ) F di i
[55/3 -62/3) 3 58/8 176/4 -2 -6
[62/3 -69/3) 2 65/8 131/6 -1 -2
[69/3 -76/3) 5 72/8 364 0 0
[76/3 -83/3) 3 79/8 239/4 1 3
[83/3 - 90/3] 12 86/8 1041/6 2 24
کل 25
• میانگین مستقیم
x F XNi i 358 8/ 2 65 8/ 5 72 825/ 3 79 8/ 1286 8/ 195325 78 12/
• میانگین غیرمستقیم با توجه به اینکه وسط، مرکز دستهها عدد 8/72 است. داریم:
A 72 8/
x A (NF id i )I 72 8/ ( 6 2 250 3 24) 7 78 12/
2- مد ( نما )
تعریف مد بصورت بیشترین تکرار برای دادههای پیوسته و طبقه بندی شده بخوبی گویا و رسا نیست و رسایی آن فقط در مورد طبقه مددار میباشد. در دادههای طبقه بندی شده، مد از طریق زیر محاسبه میشود.
Mo L Mo (d dd1 1 2 )I
اجزاء تشکیل دهنده فرمول مد عبارت است از: حد پایین واقعی طبقه مد دار= oL M
فراوانی مطلق طبقه مدار منهای فراوانی طبقه ماقبل= 1d 1 Fi Fi فراوانی مطلق طبقه مدار منهای فراوانی طبقه ما بعد= 1d 2 Fi Fi مثال2: برای مشاهدات ارائه در مثال 1 مد را حساب کنید.
L Mo 83 3/ :حل
d 1 Fi Fi 1 12 3 9
d 2 Fi Fi 1 12 0
Mo L Mo (d dd1 1 2 )I 83 3/ (9 9 12) 7 86 3/
3- چندکها
با تقسیم دامنه تغییرات به چهار قسمت مساوی به چارکها، به ده قسمت مساوی به دهکها و به صد قسمت مساوی به صدکها خواهیم رسید.
کاربرد چندکها
1- در کنترل کیفیت آماری
2- در مدیریت
3- در اقتصاد کلان و سایر علوم مشابه
3- 1 چارک:
مراحل محاسبه چندکها
1- اضافه کردن ستون فراوانی تجمعی به جدول
2- پیدا کردن محل چارک مورد نظر با استفاده از
CQ a aN4
که a= شماره چارک (1،2 یا 3) و N= تعداد کل مشاهدات.
3- پیدا کردن طبقه چارک دار و استفاده از فرمول چارک در دادههای طبقه بندی شده
aN
Q a LQ a ( 4 FFi c i 1 )I که در آن
مقدار چارک = Q a حد پایین واقعی طبقه چارک دار = LQ a فراوانی تجمعی طبقه ما قبل طبقه چارک دار = 1Fc i فراوانی مطلق طبقه چارک دار = F i
3-2 مراحل محاسبه دهکها (Da)
1- اضافه کردن F C به جدول
2- پیدا کردن محل دهک با استفاده از 10C D a aN
3- محاسبه دهک با استفاده از مراحل قبلی و فرمول دهک برای دادههای طبقه بندی شده
aN a ( 10 Fc i 1)I
D L D a F i
که در فرمول فوق
حد پایین واقعی طبقه دهک دار = L D a
فراوانی مطلق طبقه دهک دار = F i فراوانی تجمعی طبقه ما قبل طبقه دهک دار = 1Fc i فاصله طبقات = I
3-3 صدکها
صدکها را با P a نشان میدهند و مراحل محاسبه آن تقریباً مشابه دهکها و چارکها است و مقدار محاسبه شده نیز همانند سایر پارامترهای مربوط به جداول تقریبی است.
- اضافه کردن F C به جدول
2- پیدا کردن محل صدک با استفاده از 100C P a aN
3- محاسبه صدک با استفاده از مراحل قبلی و فرمول شدک برای دادههای طبقه بندی شده
(aN100 Fc i 1
P a L P a F i )I
که در فرمول فوق
حد پایین واقعی طبقه صدک دار = L P a
فراوانی مطلق طبقه صدک دار = F i فراوانی تجمعی طبقه ما قبل طبقه صدک دار = 1Fc i فاصله طبقات = I مثال3: برای مشاهدات ارائه در مثال 1 موارد زیر را حساب کنید.
الف) چارکها.
ب) دهک اول، پنجم و هفتم.
ج)صدک 25، 50 و 70. حل:
حدود طبقات فراوانی مطلق (Fi ) فراوانی تجمعی
(Fci )
[55/3 -62/3) 3 3
[62/3 -69/3) 2 5
[69/3 -76/3) 5 10
[76/3 -83/3) 3 13
[83/3 - 90/3] 12 25
کل 25
الف) 5 251
CQ 1 1425 6 25/ , Q 1 69 3/ ( 4 5 ) 7 71 05/
225 12 5/ , Q 1 69 3/ ( 24253 10) 7 75 13/
CQ 2 4 325 18 76/ , Q 1 83 3/ ( 34251213) 7 86 66/
CQ 2 4
ب)
11025 0) 7 61 13/
D 1 55 3/ ( 3
525 10
D 5 76 3/ ( 10 3 ) 7 82 13/
71025 13) 7 85 925/
D 7 83 3/ ( 12
C D 1 11025
C D 5 51025
C D 7 71025
ج)
2510025 5) 7 71 05/
P 25 69 3/ ( 5
5025 10
P 25 76 3/ ( 1003 ) 7 82 13/
7010025 13) 7 85 925/
P 25 83 3/ ( 12
C P 25 2510025 6 25/
C P 50 5010025 12 5/
C P 70 7010025 17 5/
نکته مهم : هنگام محاسبه پارامترهای مرکزی، مثل مد و چندکها (چارکها، دهکها و صدکها) باید طول و عرض طبقه مساوی باشد. به عبارت دیگر چنانچه روش طبقه بندی با تقریب صورت گرفته باشد باید از حد پایین کرانهها واقعی برای محاسبه این دسته از پارامترها استفاده شود. مثال4: سن 30 مدیر موسسه در جدول توزیع فراوانی زیر ارائه شده است.
حدود طبقات فراوانی مطلق
(Fi )
35-41 5
42 -47 10
48 -53 3
54 -59 5
60 -65 5
66 -71 2
کل 30
الف) برای مشاهدات فوق میانگین مستقیم و غیرمستقیم را محاسبه کنید.
ب) مد مشاهدات فوق را به دست آورید.
ج) میانه (چارک دوم)، دهک هشتم و صدک نودم را محاسبه کنید.
حل: با توجه به گسسته بودن حدود طبقات ابتدا کرانههای واقعی را محاسبه میکنیم.
حدود طبقات کرانههای
واقعی مرکز دسته (x i ) فراوانی مطلق
(Fi ) di فراوانی تجمعی (FCi )
35 -41 34/5 -41/5 38 5 -2/5 5
42 -47 41/5-47/5 44 10 -1/5 15
48 -53 47/5-53/5 50 3 -0/5 18
54 -59 53/5-59/5 56 5 0/5 23
60 -65 59/5-65/5 62 5 1/5 28
66 -71 65/5-71/5 68 2 2/5 30
کل 30
الف) میانگین مستقیم
x F XNi i 538 10 44 3 5030 5 56 5 62 2 68 150630 50 2/
میانگین غیرمستقیم با توجه به اینکه وسط، مرکز دستهها اعداد 50 و 56 است. داریم:
A 53
x A (NF id i )I 53 (12 5/ 15 1 5/ 302 5/ 7 5/ 5) 6 50 2/
L Mo 41 5/ (ب
d 1 Fi Fi 1 10 5 5
d 2 Fi Fi 1 10 3 7
Mo L Mo (d dd1 1 2 )I 41 5/ (5 5 7) 6 44
ج) میانه (چارک دوم): 302
CQ 2 2430 15, Q 1 47 5/ ( 4 3 15) 6 47 5/ :دهک هشتم
830 23
C D 8 8 1030 24 D 7 59 5/ ( 10 5 ) 6 60 7/
صدک نودم:
C P 90 9010030 27 P 25 59 5/ ( 5 23) 6 64 3/
پارامترهای پراکندگی در دادههای طبقه بندی شده
1- انحراف متوسط از میانگین (AD)
2- دامنه میان چارکی (IQR)
3- انحراف چارکی (SIQR)
4- واریانس (2x ) که شامل روش مستقیم و غیرمستقیم میشود.
5- واریانس تصحیح شده ( 2c)
1- انحراف متوسط از میانگین
فرمول محاسبه انحراف متوسط از میانگین در دادههای طبقه بندی به شکل زیر میباشد در این فرمول
F i فراوانی مطلق طبقه i ام میباشد.
AD F i NX i x
مثال5: برای مشاهدات مثال1، انحراف متوسط ازمیانگین را جساب کنید.
حل:
AD 3 | 58 8/ 78 12/ | 2 | 65 8/ 78 12/ | 5 | 72 8/ 2578 12/ | 3 | 79 8/ 78 12/ | 12 | 86 8/ 78 12/ | 219 5425/ 8 78/
2- دامنه میان چارکی
برای محاسبه دامنه میان چارکی مانند قبل از فرمول زیر استفاده میشود.
IQR Q3 Q1
مثال6: برای مشاهدات مثال1، دامنه مین چارکی را جساب کنید.
IQR Q3 Q1 86 66/ 71 05/ 15 61/
3- انحراف چارکی
برای محاسبه انحراف چارکی مانند قبل از فرمول زیر استفاده میشود.
SIQR Q3 2 Q1
مثال7: برای مشاهدات مثال1، انحراف چارکی را جساب کنید.
SIQR Q3 2 Q1 86 66/ 271 05/ 15 612/ 7 805/
نکته: از پارامترهای پراکندگی دامنه میان چارکی و انحراف چارکی زمانی استفاده میشود که دنبالههای توزیع نامعین و باز باشد ( در این حالت محاسبه میانگین و واریانس امکان پذیر نیست.)
مثال8: در کشور آمریکا، در سالهای 1900 تا 1973، تعداد تلفات انسانی در هر طوفان بزرگی ثبت شده و فراوانی این تلفات، به قرار زیر بوده است:
تعداد مرگ فراوانی مطلق
(Fi )
24 و کمتر 4
25 -49 16
50 -74 16
75 -99 11
100 -149 6
150 -199 2
200-249 4
250 و بیشتر 1
کل 60
برای دادههای فوق پارامترهای پراکندگی را محاسبه کنید.
حل: با توجه به مشخص نبودن حدود در طبقات اول و هشتم، امکان محاسبه میانگین و مرکز دستههای این طبقات وجود ندارد بنابراین ما از دامنه میان چارکی و انحراف چارکی برای محاسبه پارامترهای پراکندگی استفاده میکنیم.
برای محاسبه چارکها با توجه به گسسته بودن طبقه بندی ابتدا کرانههای واقعی را به دست میآوریم.
تعداد مرگ کرانههای واقعی فراوانی مطلق (Fi ) فراوانی تجمعی (Fci )
24 و کمتر 5/24 و کمتر 4 4
25 -49 24/5-49/5 16 24
50 -74 49/5-74/5 16 40
75 -99 74/5-99/5 11 51
100 -149 99/5-148/5 6 57
150 -199 149/5-199/5 2 59
200-249 199/5-249/5 4 563
250 و بیشتر 5/249 و بیشتر 1 60
کل 60
I 49 25 1 25
1 160 15, Q 1 24 5/ ( 1460164)25 40 125/
CQ 4
3 360 45, Q 3 74 5/ ( 346011 36)25 94 95/
CQ 4
IQR Q3 Q1 94 95/ 40 125/ 54 825/
SIQR Q3 2 Q 94 95/ 2 40 125/ 54 825/2 27 41/
4- واریانس
همانطور که بیان شد واریانس در دادههای طبقه بندی شده به دو صورت مستقیم و غیرمستقیم محاسبه میشود.
• روش مستقیم
واریانس به روش مستقیم در دادههای طبقه بندی شده با استفاده از فرمول زیر محاسبه میشود.
x2 F i (XN i x )2
به منظور سادگی در محاسبات، به جای فرمول فوق میتوان از فرمول زیر جهت محاسبه واریانس به روش مستقیم برای دادههای طبقه بندی شده استفاده کرد. ( میتوان نشان داد هر دو فرمول معادل هستند.)
x2 FNi X i 2 2X
• روش غیر مستقیم
واریانس به روش مستقیم در دادههای طبقه بندی شده با استفاده از فرمول زیر محاسبه میشود.
d
x2 I 2 F i i2 F id i 2
N ( N )
مثال9: برای مشاهدات مثال1، واریانس را به دو روش مستقیم و غیرمستقیم محاسبه کنید.
حل: محاسبه واریانس مستقیم با استفاده از فرمول اول
x2 3(58 8/ 78 12/ )2 2 (65 8/ 78 12/ )2 5 (72 8/ 2578 12/ )2 3 (79 8/ 78 12/ )2 12 (86 8/ 78 12/ )2 2477 4425/ 99 0976/
محاسبه واریانس مستقیم با استفاده از فرمول اول
x2 358 8/ 2 2 65 8/ 2 5 72 825/ 2 3 79 8/ 2 1286 8/ 2 78 12/ 2 155045 825 / 78 832/ 99 0976/ x x2 99 0976/ 9 95/ و انحراف معیار مشاهدات برابر خواهد بود با
محاسبه واریانس به روش غیرمستقیم
x2 4972(365 )4(219)12 52599 09760 / 3 1 124 (3 ( 2) 2 ( 1)25 5 0 3 1 122)2
25 25
5- واریانس تصحیح شده ( 2c):
در دادههای طبقه بندی شده برای محاسبة میانگین و واریانس از نمایندة طبقات استفاده میشود نتیجة این عمل ممکن است دارای اختلاف با مقادیر واقعی دادهها باشد در میانگین اشتباه ناشی از این تقریب به علت مثبت و منفی بودن اشتباهات جبران میشود از این رو از مجموع خطاها صرفنظر میگردد. در مورد واریانس چون خطاهای مثبت و منفی به توان دو میرسد خطاها یکدیگر را خنثی نمیکنند بنابراین مقدار بدست آمده برای واریانس بیش از مقدار واقعی است برای تصحیح این اشتباه، شیارد رابطة زیر را تعریف کرد که در آن صورت مقدار بدست آمده دقیقتر از واریانس خواهد بود
I فاصلة طبقات 2c2 2x 12I
باید توجه داشت این تصحیح در مواردی به کار میرود که اولاً متغیر پیوسته باشد ثانیاً تعداد N دست کم هزار باشد ثالثاً توزیع فراوانی از نوع متقارن یا اندکی متقارن باشد.
مثال10: در مورد مشاهدات مثال 1، واریانس تصحیح شده را محاسبه کنید.
c2 2x I122 99 0976/ 7122 95 01/
عملیات جبری میانگین و واریانس
اگر جامعه آماری از ترکیب چند جامعه مستقل با میانگینها و واریانسهای مشخص تشکیل شده باشد، میتوان میانگین و واریانس جامعه کل را بدست آورد.
• میانگین حسابی جامعه کل
N 1N1 1N N22 2 ......NNKKK NN ii
N i = تعداد مشاهدات جامعه i ام برای i 1 2, ,...,k N= تعداد مشاهدات جامعه کل که N N 1 N 2 ... N k
i= میانگین جامعه i ام برای i 1 2, ,...,k
• واریانس جامعه کل
2 N ii2 N i (i )2
N N
که در آن
2i = واریانس جامعه i ام برای i 1 2, ,...,k N = تعداد مشاهدات جامعه کل N i = تعداد مشاهدات جامعه i ام برای i 1 2, ,...,k
= میانگین جامعه کل
i = میانگین جامعه i ام برای i 1 2, ,...,k
مثال11: میانگین و واریانس نمرات 3 کلاس در درس آمار به صورت زیر است میانگین و وایانس کل کلاسها را محاسبه میکنیم.
کلاس 1 2 3
میانگین 12 14 18
واریانس 9 9 4
تعداد افراد 10 10 5
Ni i
N 14
2 Ni i2 Ni (i )2
N N
8 12/8
• اهمیت کاربرد انحراف معیار
یکی از موارد استفاده از انحراف معیار تعیین درصد دادههایی است که در محدودهای حول میانگین قرار میگیرند و در قضیهای با نام چبیشف به صورت زیر اثبات شده است.
قضیه چبیشف:در هر توزیع آماری حداقل 1 k12 % (درصد) مشاهدات در فاصلة k قرار
k k
x x x
مثال 12) فرض کنید توزیع قد دانشجویان کلاسی دارای میانگین 166 و واریانس 16
الف) فاصلهای را نسبت به میانگین محاسبه کنید که حداقل قد 75 درصد افراد را دربرگیرد.
ب) در فاصلة 173-159 قد حداقل چنددرصد دانشجویان قرار میگیرد.
حل :
الف) طبق قضیه چبیشف، در هر توزیع آماری حداقل 1 k12 % (درصد) مشاهدات در فاصلة
k قرار میگیرند در نتیجه با توجه به سوال ما میخواهیم
1 k12 0 75/ k12 0 25/ k 2 4 k 2
x 166 2x 16 x 16 4
k 166 2 4 (158 174, )
ب :
k159166k41594k 7k
1 k12 1 1 2 1 0/6710067%
( )
یعنی 67 درصد قد افراد در این فاصله قرار دارد.
پارامترهای تعیین انحراف از قرینگی
سوال: در هنگام مقایسه دو یا چند جامعه، در صورت مساوی بودن پارامترهای مرکزی و پراکندگی، آیا میتوان گفت دو جامعه با هم برابرند؟
جواب: لزوما دو جامعه با هم برابر نیستند و برابر بودن آنها بستگی به نوع توزیع مشاهدات حول میانگین دارد.
مفهوم چولگی
اگر دم توزیع جامعه به سمت راست باشد، توزیع را چوله به راست و در صورت عکـس، آن را چوله به چپ مینامند. چولگی توزیعها در مقایسه با توزیع متقارن معین میشود.
انواع حالات توزیعها بر اساس میزان چولگی
1- متقارن ( نرمال ) : مد = میانه = میانگین (مقدار ضریب چولگی (SK) برابر صفر است.)
2- چـولـه به راسـت : مد > میانه > میانگین (مقدار ضریب چولگی (SK) مثبت است.)
3- چـولـه بـه چــپ : مد < میانه < میانگین (مقدار ضریب چولگی (SK) منفی است.)
x MdMo چوله به x MdMo متقارن x MdMo چوله به
چپ راست
تفسیر مقادیر SK
قدرمطلق ضریب چولگی نشان دهندة میزان اختلاف جامعة آماری با توزیع نرمال از نظر قرینگی است بدیهی است که هر چه sk بزرگتر باشد اختلاف جامعة آماری با توزیع نرمال از نظر قرینگی بیشتر خواهد بود به طوریکه :
1- /0 1SK ، جامعه از نظر قرینگی تقریباً نرمال است.
2- /0 5 SK /0 1، جامعه از نظر قرینگی تفاوت اندک با توزیع نرمال دارد.
3- /0 5SK ، جامعه از نظر قرینگی تفاوت فاحش با توزیع نرمال دارد.
محاسبه ضریب چولگی ( SK )
1- ضریب چولگی گشتاوری
2- ضریبهای چولگی پیرسون
3- ضریبهای چولگی چندکی که شامل ضریب چولگی چارکی و ضریب چولگی صدکی است.
• ضریب چولگی گشتاوری
برای محاسبه ضریب چولگی گشتاوری از فرمول زیر استفاده میشود.
SK rx33
که در آن 3(r3 F i (XN i x ، گشتاور مرتبه سوم به مبدأ میانگین و x، انحراف معیار است.
• ضریب چولگی پیرسون
(X Mo)
S K 1 X 1 فرمول شماره .1
3(X Md )
2. فرمول شماره 2 S K 2 X که در روابط فوق Mo، مد و Md میانه است.
مثال 13: برای مشاهدات مثال 1 چولگی گشتاوری و چولگی پیرسون را محاسبه کنید.
حل: ضریب چولگی گشتاوری
3
r F (X i x ) 18265 16
3 i N 25 / 730 61/ ,x2 99 0976/ x 9 95/
SK rx33 /3 0 74/
ضریب چولگی پیرسون
(X Mo) (78 12/ 86 3/ ) 0 822/
S K 1 X 9 95/
S K 2 3(XX Md ) 3(78 12/ / 75 13/ ) 0 901/
9 95
با توجه به آنکه مقدار /0 5SK ، میتوان گفت جامعه از نظر قرینگی تفاوت فاحش با توزیع نرمال دارد.
• ضرایب چولگی چندکی
1. SK Q QQ Q3 23Q Q 2 1 1 ضریب چولگی چارکی
2. ضریب چولگی صدکی 10 10SK P P 90P290P PP50 که در آن Qi چارک iام و Pi، صدک iام است.
نکته: چولگی چندکی زمانی که محاسبه میانگین و واریانس برای توزیع امکانپذیر نباشد. کاربرد دارد.
مثال 14: برای مشاهدات مثال 8 چولگی چارکی و صدکی را محاسبه کنید.
حل: ضریب چولگی چارکی
260 20
CQ 2 2 460 30, Q 2 49 5/ ( 4 16 )25 65 125/
SK Q Q Q QQ Q3 23 2 1 1 0 088/
ضریب چولگ صدکی
P 1060 , 10 / ( 1060 4) /
C 10 100 6 P 24 5 1016 25 27 625
C P90 9010060 54, P90 149 5/ ( 2 53)25 162 P50 Q2 65 125/
SK P P 90P290P PP50 10 10 162 216265 125/27 625/ 27 625/ 0 44/
پارامترهای تعیین انحراف از کشیدگی
این پارامترها برای مقایسه توزیع جوامع مورد نظر با توزیع جامعه نرمال به لحاظ کشیدگی (کوتاهی و بلندی توزیع) مورد استفاده قرار میگیرد.
انواع توزیع به لحاظ کشیدگی و مقدار ضریب ( E ) آن
1-از نظر کشیدگی (بلندی توزیع) مساوی توزیع نرمال ( 0E= )
2- از نظر کشیدگی (بلندی توزیع) بلندتر از توزیع نرمال ( E<0 )
3- از نظر کشیدگی (بلندی توزیع) کوتاه تر از توزیع نرمال ( E>0 )
E0
E0
Mdx Mo
• تفسیر ضریب کشیدگی ( E )
1- اگر /0 1E توزیع جامعه از نظر کشیدگی تقریبا نرمال است.
2- اگر /0 5 E /0 1 توزیع جامعه از نظر کشیدگی نسبتاً بلندتر از نرمال است.
3- اگر /0 5E توزیع جامعه از نظر کشیدگی کاملاً کشیده تر از نرمال است.
• انواع ضرایب کشیدگی
1- ضریب کشیدگی گشتاوری ؛
2- ضریب کشیدگی چندکی ؛
• ضریب کشیدگی گشتاوری
این ضریب گشیدکی با استفاده از گشتاور مرتبه چهارم نسبت به مبدأ میانگین محاسبه میشود که فرمول آن به صورت زیر ارائه میشود.
E rX44 3
.و 3 عددی ثابت است r 4 F i (XN i x )4 که
مثال15: برای مشاهدات مثال 1 کشیدگی گشتاوری را محاسبه کنید.
r 4 F i (XN i x )4 53619725 21447 88/
E rX44 3 4 3 2 19/ 3 0 81/
با توجه به اینکه /0 5 E /0 1 میتوان گفت، توزیع جامعه از نظر کشیدگی نسبتاً بلندتر از نرمال است.
• ضریب کشیدگی چندکی
این ضریب گشیدکی با استفاده از انحراف چارکی و صدکهای دهم و نودم محاسبه میشود که فرمول آن به صورت زیر ارائه میشود.
E P PSIQR90 P 10 0 263/
نکته:این ضریب گشیدگی مخصـوص توزیـعهایی که بالاجبار با استـفاده از چـندکها تـوصـیف میشـوند. مثال 16: برای مشاهدات مثال 8 ضریب کشیدگی چندکی را محاسبه کنید.
/0 42E P PSIQR90 P 10 0 263/ 162 27 4127 625/ / 0 263/ با توجه به اینکه /0 5 E /0 1، میتوان گفت توزیع جامعه از نظر کشیدگی نسبتاً بلندتر از نرمال است.
ر این فصل دانشجو با برخی از مفاهیم احتمال و انواع احتمالات آشنا میشود. مفاهیمی چون فضای نمونه، پیشامد و نیز اصول شمارش و جایگشتها و ترکیبها بیان شده است. و نیز مفهوم احتمال، تابع احتمال، اصل موضوع احتمال شرطی استقلال دو پیشامد قانون و احتمال کل توضیح داده میشود.
مفاهیم اساسی احتمال
مفهوم احتمال (P): احتمال یعنی شانس وقوع یک پیشامد خاص.
احتمال عینی: احتمال عینی، ثابت و مقدار آن از قبل مشخص است و به عقاید اشخاص بستگی ندارد.
(احتمال 6 آمدن تاس در یک بار پرتاب)
احتمال ذهنی: احتمال ذهنی، متغیر و وابسته به نظر اشخاص است. (مثال: پاسخ مسافران در مورد احتمال تاخیر پرواز تهران-تبریز)
آزمایش : فعالیتی که نتیجه آن از قبل مشخص نیست ولی کل حالات ممکن آن معلوم است، مثل پرتاب یک سکه، که معلوم نیست دقیقاً شیر خواهد آمد یا خط
فضای نمونه :مجموعه پیامدهای ممکن یک آزمایش را فضای نمونه آن آزمایش میگویند .فضای نمونه را با S نشان میدهند.
مثال1: فضای نمونه پرتاب یک تاس
S {1 2 3 4 5 6, , , , , }
فضای نمونه محدود: یعنی این که فضای نمونه تعداد کمی عضو داشته باشد. (مثل فضای نمونه پرتاب یک تاس)
فضای نمونه نامحدود: یعنی اینکه فضـای نمونه آزمایش ( تعداد اعضاء آن ) نامتناهی است. مثال2:
یک سکه را آنقدر پرتاب میکنیم تا شیر ظاهر شود. فضای نمونه را بنویسید.
حل: اگر H نماد شیر و T نماد خط باشد داریم.
S H TH TTH, , ,...
فضای نمونه گسسته و پیوسته : اگر اعضای فضای نمونه آزمایش قابل شمارش باشد، آن را فضای نمونه گسسته ولی اگر فضای نمونه آزمایشی بصورت اعداد اعشاری باشند آن را پیوسته مینامند.
مثال3: تعداد پرتابهای یک تاس تا آمدن 6 نمونهای از فضای نمونه گسسته و نامتناهی است.
S {1 2 3, , ,...}
فضای نمونه طول عمر لامپهای تولیدی یک کارخانه نمونهای از فضای نمونه نامتناهی و پیوسته است.
S {x 0}
فضای نمونه ظول عمر نوعی لامپ که حداکثر عمر آن 1780 ساعت است. نمونهای از فضای نمونه متناهی و پیوسته است.
S {0 x 1780}
پیشامد : به هر یک از زیر مجموعههای فضای نمونه، یک پیشامد گفته میشود هر پیشامد را با یکی از حروف بزرگ انگلیسی مثل A و B و C و . . . نشان میدهند.
مثال4: B پیشامد ظاهر شدن عدد زوج در پرتاب یک تاس
SB {{1 2 3 4 5 62 4 6, , , , ,, , } }
پیامدهای مقدماتی هم شانس : پیامدهای مقدماتی یا پیشامدهای اولیه هم شانس یعنی این که تمام پیشامدهای اولیه در آزمایشی دارای شانس وقوع برابر باشند. (مثال: احتمال رو آومدن هر سک از اعداد 1 تا 6 در پرتاب یک تاس)
احتمال یک پیشامد
• احتمال یک پیشامددر پیامدهای مقدماتی هم شانس
احتمال وقوع پیشامدی مثل A برابر میشود با تعدادهای عضوهای پیشامد A به تعداد عضوهای فضای نمونه
(( ))P A( ) n An S مثال4: احتمال پیشامد ظاهر شدن عدد زوج در پرتاب یک تاس.
P B( ) 3 1
6 2
• احتمال یک پیشامد در پیامدهای مقدماتی غیر هم شانس
برای پیشامدی مثل A فراوانی نسبی پیشامد A درNتکرار = P(A) بشرطی که N به سمت بی نهایت میل کند.
خواص اولیه احتمال
برای هر پیشامدی مثل A (چه هم شانس و چه غیر هم شانس)
12 ( )P S0 P A( 1) 1
قواعد شمارش این قواعد عبارتند از :
1- قاعده ضرب 2- جایگشت (ترتیب)
3- ترکیب 4- افرازهای (تفکیکهای) مرتب کاربردهای قواعد شمارش
از این قواعد در وضعیتهایی استفاده میشود که فهرست نمودن تمام حالات ممکن آزمایش مقدور نمیباشد، لذا فقط به ذکر تعداد حالات ممکن و مختلف اکتفا میشود.
1- اصل اساسی شمارش
اساسیترین اصل در شمارش » قاعده ضرب « است و این اصل مختص آزمایشهایی است که در آنها عملیات در چند مرحله ( مثلاً K ) مرحله انجام میپذیرد.
قاعده ضرب : طرق ممکن انجام عمل در آزمایشی که مرحله اول آن به 1n طریق و . . . مرحله K ام آن به n K طریق انجام میگیرد، عبارت خواهد بود از :
n n1 2 ...n K
مثال5: اگر دایره بازاریابی و فورش شرکتی بخواهد یکی از 5 متن تهیه شده را با یکی از وسیلههای تبلیغاتی ( رادیو، تلویزیون، مجله و روزنامه) آگهی کند، این کار را به چند طریق میتواند انجام دهد.
حل: با توجه به اینکه این کار در 2 مرحله انجام میشود به طوری که 5n1 و 4n2 بوده و این دو مرحله از هم مستقل هستند. پس تعداد کل حالات برابر است با:
n1 n2 5 4 20
نمودار درختی : این نمودار روشی است منظم برای نشان کل حالات ممکن در آزمایشاتی که عملیات
در آنها طی چندین مرحله انجام میپذیرد. ( مکمل قاعده ضرب )
مثال 6: جهانگردی میخواهد با پای پی اده یا با دوچرخه یا با ماشین به یکی از 5 کشور ایران، چین، یونان، ترکی ه یا ایتالیا سفر کند این جهانگرد به چند طریق میتواند این مسافرت را انجام دهد.
جواب : وی طریقة مسافرت را به 3n1 طریق میتواند انتخاب کند و کشور مورد نظر را به
5n2 طریق انتخاب کند بنابراین تعداد طرقی که میتواند انتخاب کند عبارتند از :
15n1n2 35 نمودار درختی مربوط در شکل زیر رسم شده است.
تعریف فاکتوریل: فاکتوریل که برای عددی مانند n با نماد »n!« نشان میدهیم عبارت است از حاصلضرب اعداد 1 تا n، که در این صورت داریم :
1!1 2!212 3!3216 4!432124 ,....
و بنا به تعریف (!0) برابر 1 میباشد.
2- جایگشت ( ترتیب )
یعنی تعداد طرقی که میتوان r شی را از بین n شی انتخاب نمود بطوریکه r n و ترتیب قرار گرفتن اشیاء نیز مهم باشد
حالات مختلف پیدا کردن جایگشت
1. تعداد کل جایگشتهای n شی متمایز
2. تعداد کل جایگشتهای n شی نامتمایز
2. تعداد جایگشتهای r شی انتخابی از بین n شی متمایز
1. تعداد کل جایگشتهای n شی متمایز
1- در صورت ردیفی بودن بشکل 1n! n (n 1)(n 2) ...
(n 1)! (n 1) (n 2)... 1 در صورت دایرهای بودن -2
2. جایگشتهای n شی نامتمایز
n1 !n2n! ...! nk !
که از n شی، 1n تای آنها از نوع اول، 2n تای آنها از نوع دوم و ....و nk تای آنها از نوع k ام است. و
.است n1 n2 ... nk n
3- جایگشتهای r شی از بین n شی ! (P nr (n n!r
که r و n هر دو متمایز و r < n
نکات مهم در محاسبه جایگشتها ( ترتیبها )
1- توجه به تعداد اشیاء و حجم انتخابی از بین آنها
2- توجه به ردیفی یا دایرهای بودن اشیاء
3- توجه به متمایز یا نامتمایز بودن اشیاء مثال7: به چند طریق میتوان با حروف B، C، D،E و A یک کلمه سه حرفی ساخت؟
60 3 4 5 52!! !(3!5 5) مثال8: از بین 15 تیم شرکت کننده در مسابقه فوتبال به چند طریق میتوان سه تیم رتبههای اول، دوم و سوم را به دست آورد.
(1515!3)! 1512!! 151413 2730
مثال9: تعداد جایگشتهای حروف کلمه book را به دست آورید.
(جایگشت با n شی نامتمایز) 12 !
مثال10: به چند طریق میتوان یک کلاس 20 نفری را به دستههای 3، 4، 6 و 7 نفری تقسیم کرد.
(جایگشت با n شی نامتمایز)
3- ترکیب
تعداد طرق انتخـاب r شی متمـایز از بین n شـی بشرطی که ترتیب قرار گرفتن اشیاء بی اهمیت باشد.
که تعداد حالات ممکن را میتوان از فرمول زیر محاسبه کرد.
( nr ) (n nr!)! ! r n n( 1)...(r!n r 1)
استفاده از قاعده ضرب در ترکیب
n K n 2 n 1
اگر ترکیب اول به شکل r 1 ترکیب دوم بصورت r 2 و . . . ترکیب آخر به شکل r K باشد در آن صورت تعداد کل طرق برابر است با
n 1 n 2 n K
r 1 r 2 ... r K
ویژگیهای ترکیب r شی از n شی
n n
1 n (٢ 0 1 (1
n n
n 1 n (٤ n 1 (٣
مثال11: از بین 15 تیم شرکت کننده در مسابقه فوتبال به چند طریق میتوان سه تیم را انتخاب کرد.
455153 (15 153!)! !3 153142 13 مثال12: به چند طریق میتوان از 12 کتاب که 5 تای آن آمار و بقیه ریاضی هستند، یک کتاب آمار و 2 کتاب ریاضی را به عنوان کتاب سال برگزید؟
51 27 5 21 105
4- افرازهای مرتب
گاهی تعداد طرقی که میتوان مجموعة n شیئی را به k زیرمجموعه با 1n شی در مجموعه اول 2n شی در مجموعه دوم، ... و nk شی در مجموعه k افراز کرد برابر است با :
n1، n2،n...،n k n1! n2n!!... nk !
.است n1 n2 ... nk n که در آن
ویژگیها افراز :
1- تفکیک n شی به گونهای خاص
2- در حکم یک مجموعه بودن هر ترکیب
3- مهم نبودن ترتیب اشیاء در هر زیر مجموعه
مثال13: به چند طریق میتوان 9 اسباب بازی را بین 4 بچه تقسیم کرد به شرط آنکه به کوچکترین بچه 3 اسباب بازی و به هر کدام از بچههای دیگر 2 اسباب بازی برسد؟ 756093 2 2 2, , , 3 2 2 2! ! ! !9!
عملیات روی پیشامدها و قواعد احتمال
نمودار ون : در این نمودار به منظور نشان دادن پیشامدها،کل فضای نمونه در قالب مستطیلی ارائه شده و هر پیشامدی قسمتی از این مستطیل را به خود اختصاص میدهد.
احتمال پیشامدی مانند A در نمودار ون برابر است با سطحی که پیشامد A از S (فضای نمونه) اشغال کرده است یا بربر با نسبت تعداد اعضای A به S است.
دو پیشامد نا سازگار : دو پیشامد را در صورتی » نا سازگار « گویند که امکان وقوع همزمان نداشته باشند یعنی با وقوع یکی، دیگری امکان وقوع نداشته باشد.( مثل شب و روز)
نمودار ون برای دو پیشامد نا سازگار به صورت زیر است. نمودار نشان میدهد که پیشامدهای A و B هیچ وجه اشتراکی با هم ندارند .
دو پیشامد سازگار : دو پیشامدی را گویند که وقوع یکی مانع وقوع دیگری نیست بعبارتی این دو پیشامد دارای حداقل یک عضو مشترک هستند.
نمودار ون برای دو پیشامد سازگاربه صورت زیر است. محل تلاقی دو پیشامد، نقطه مشترک آنهاست.
اجتماع دو پیشامد: اجتماع دو پیشامدی مثل A و B، مجموعه تمام عضوهایی است که در A یا در B یا هم در A و هم در B قرار دارند.اجتماع دو پیشامد A و B را با A B نشان میدهند . وقوع A B یعنی این که حد اقل یکی از دو پیشامد مذبور رخ داده است.
نمودار ون برای A B به صورت زیر است.
اشتراک دو پیشامد: اشتراک دو پیشامدی مثل A و B را با A ∩ Bنشان میدهند . وقوع A B یعنی این که هر دو پیشامد A و B رخ داده است.
نمودار ون برای اشتراک دو پیشامدبه صورت زیر است.
یعنی این که هم پیشامد A و هم پیشامد B رخ داده است.
متمم یک پیشامد : متمم پیشامدی مثل A که باA C نشان داده میشود مجموعه تمام عضوهایی است که در فضای نمونه است ولی در خود پیشامد A نیست
نمودار ون برایA C به صورت زیر است. وقوع متمم A C ) A ) به معنی عدم وقوع پیشامد A میباشد .
برخی قواعد احتمال
1. در صورتیکه A و B دو پیشامد از فضای نمونة S باشند و A زیر مجموعة B نیز باشد (AB) چون A دارای تعداد عضوهای کمتر یا مساوی B میباشد احتمال وقوع پیشامد A کوچکتر یا مساوی احتمال وقوع پیشامد B است یعنی
P(A)P(B)
2. از آنجایی که AC قسمتی از فضای نمونه است که در A نیست اجتماع A و AC برابر فضای نمونه است یعنی AAC S و مجموع احتمال آنها برابر با احتمال فضای نمونه یعنی یک خواهد بود
: بنابراین P(A) P(AC )1
P(AC )1P(A)
3. احتمال اجتماع دو پیشامد A و B را از قاعدة جمع احتمالات بدست میآوریم :
P( AB) P(A) P(B) P(AB)
4. در صورتی که دو پیشامد ناسازگار باشند چون دو پیشامد ناسازگار ,اشتراکی ندارند
(A B ) و در نتیجه 0P A( B ) ، احتمال اجتماع آنها عبارتست از:
P(AB) P(A) P(B)
مثال14: اگر برای خانواده ای، احتمال دارا بودن یک دستگاه کامپیوتر، یک دستگاه لپ تاپ و یا هردو به ترتیب 86/0، 35/0 و 29/0 باشد. احتمال اینکه این خانواده یکی از دو نوع یا هر دو نوع دستگاه (حداقل یکی از دو نوع دستگاه) را داشته باشند. چقدر است؟
حل: اگر A، پیشامد این باشد که خانواده مزبور دارای یک دستگاه کامپیوتر است. B، پیشامد این باشد که خانواده مزبور دارای لپ تاپ است. داریم:
/0 29P A( ) 0 86/ , P B( ) 0 35/ , P A( B ) بنابراین احتمال مورد نظر (حداقل یکی از دو نوع دستگاه را دارا باشند.) برابر است با:
P A( B ) 0 86/ 0 35/ 0 29/ 0 92/
مثال15: خودرویی در کنار خیابانی متوقف شده است. با احتمال 23/0، ترمزهایش معیوب است و با احتمال 24/0 فرسودگی شدید تایر دارد. همچنین با احتمال 38/0 ترمزهایش معیوب یا فرسودگی شدید دارد. احتمال اینکه این اتومبیل ترمزهایش معیوب بوده و فرسودگی شدید تایر داشته باشد. چقدر است؟ همینطور احتمال اینکه خودرو مورد نظر ترمزهایش معیوب نباشد چقدر است؟
حل: اگر B پیشامد این باشد که خودرو مورد نظر ترمزهایش معیوب باشد و T پیشامد این باشد که تایرهایش فرسوده باشد. داریم:
/0 38P B( ) 0 23/ , P T( ) 0 24/ , P BUT( ) بنابراین احتمال اینکه هم ترمزش معیوب باشد هم تایرهایش فرسوده باشند برابر است با:
/0 09/ P B( 0 23/T)0 24/ 0 23/P B(0 24/ T0 38)/ 0 38 و احتمال اینکه ترمزهایش معیوب نباشد برابر است با:
P B( c ) 1 P B( ) 1 0 23/ 0 77/
احتمال شرطی
اگر پیشامدی همانند A به پیشامد دیگری همانند B مربوط باشد و بدانیم پیشامد B به وقوع پیوسته است در این صورت احتمال وقوع A، به احتمال وقوع A به شرط P(A B)) B) تغییر مییابد که آنرا احتمال شرطی مینامیم.
اگر A و B دو پیشامد دلخواه از فضای نمونه S باشد و 0P(B) احتمال وقوع A به شرط B برابر است با :
P(AB) P(PA(B)B)
مثال16: دو تاس را پرتاب میکنیم در صورتی که بدانیم مجموع اعداد ظاهر شده برابر 6 است. مطلوب است احتمال اینکه یکی از تاسها عدد 2 را نشان دهد.
حل: تمام حالات پرتاب دو تاس برابر است با:
S {(1 1, ),( , ),...,( , ),...,( ,1 2 1 6 6 6)}
اگر B پیشامد این باشد که یکی از تاسها عدد 2 را نشان دهد و C پیشامد این باشد که مجموع اعداد ظاهر شده برابر 6 است. داریم:
{(1 5 5 1 {(4 42 2, ),( ,3 23 4)}CB {(C2 4, ),( , ),( , ),( , ),( , در نتیجه احتمال مورد نظر برابر است با:
P B C( | ) P B(P C()C )
قانون ضرب احتمالات
با استفاده از احتمـال شرطی میتوان قانـون ضرب را برای محاسبه احتمال اشتراک پیشامدها بشرح زیر بیان نمود.
P A( B )
P A B( | ) P A( B ) P A B P B( | ) ( )
P B( )
P A( B )
P B A( | ) P A( B ) P A P B A( ) ( | )
P A( )
قانون ضرب احتمالات برای بیش از دو پیشامد نیز کاربرد دارد. فرمول ضرب احتمالات برای سه پیشامد این گونه است :
P(ABC)P(A)P(B A)P(C / AB)
مثال17: فرض کنید جعبهای شامل 10 لامپ میباشد که در بین آنها 4 لامپ معیوب وجود دارد. دو لامپ پشت سر هم و بدون جایگذاری استخراج میکنیم. احتمال این که هر دو لامپ معیوب باشند چقدر است ؟ حل : پیشامد اولی ناسالم :A پیشامد دومی ناسالم :B
p A( ) 4 , p B A( | ) 3
p A( 10 B ) p B A p A( | ). (9 ) 3 4 4 3 12
9 10 10 9 90
حال اگر سه لامپ استخراج شود احتمال سالم بودن هر سه لامپ را حساب کنید.
حل : پیشامد اولی سالم :A پیشامد دومی سالم :B پیشامد سومی سالم:C
P A( B C ) 106 95 84
دو پیشامد مستقل
دو پیشامد را » مستقل « میگوییم، در صورتی که وقوع یا عدم وقوع یکی در وقوع و یا عدم وقوع دیگری هیچ تأثیری نداشته باشد
زمانی که دو پیشامد A و B از هم مستقل باشند هیچ تأثیری بر روی هم ندارند برای محاسبه احتمال اشتراک آنها بشکل زیر عمل میشود :
P A B(P A(| ) BP A)( P A B P B) (, P B A|( )| () ) P B(P A() B ) P A P B( ) ( )
شرط ناسازگار بودن دو پیشامد 0A B (P A B )
شرط مستقل بودن دو پیشامد ( ) ( )P A B ) P A P B)
پیشامدها نسبت به هم میتواند، حالت سازگار و مستقل، سازگار و غیر مستقل، ناسازگار و غیر مستقل و . . . داشته باشند.
قضیه بیز
این قضیه پژوهشگران را در تجدید نظر احتمالات، در صورت دسترسی به اطلاعات جدید، کمک میکند فرمول این قضیه در حالتی که دو عامل مدنظر باشد به صورت زیر است..
P A B( | ) P A P B A( P B) (( ) | )
در بسیاری از موارد بیش از 2 عامل نقش تعیین کنندهای در وقوع پیشامدی دارند اگر 1A و
2A ، ... و A k نشان دهندة K حادثة ناسازگار باشند که میتوانند حادثة B را باعث شوند آنگاه احتمال اینکه Ai عامل وقوع باشد برابر است با :
P ( A i | B) P (PA (iB) B) P (A ) P (B | A ) .... PP( A( Ai)iP) P( B(B| |AAi)i) ... P ( A ) P ( B | A )
1 1 K K
احتمالات پسین و پیشین :به احتمال وقوع پیشامدی قبل از کسب اطلاعات جدید » احتمال پیشین « و به احتمال وقوع آن پیشامد بعد از کسب اطلاعات جدید » احتمال پسین « میگویند.
مثال18: فرض کنید میدانیم 30% دانشجویان چهارم،80 %دانشجویان سال سوم،70 %دانشجویان سال دوم و50% دانشجویان سال اول از کتابخانه استفاده میکنند .اگرازهمهی دانشجویان، 25% سال اول، 25% سال دوم،20% سال سوم و 30% سال چهارم باشند، در اینصورت
الف) احتمال اینکه دانشجویی از کتابخانهی مرکزی استفاده کند چقدر است ؟
ب) دانشجوی سال دومی انتخاب میشود چقدر احتمال دارد از کتابخانه مرکزی استفاده کند؟
حل: تعریف میکنیم
پیشامد اینکه دانشجویی از کتابخانهی مرکزی استفاده کند :A پیشامد اینکه دانشجوی سال اول باشد : F پیشامد اینکه دانشجوی سال دوم باشد :O پیشامد اینکه دانشجوی سال سوم :J پیشامد اینکه دانشجوی سال چهارم باشد: E
P FP A F(( )| )0 25/ 0 5,/ ,P O(P A O() |0 25/ ) , P J0 7/ ,( )P A J(0 2/ | , )P E(0 8/) , 0 3P A E/( | ) 0 3/
الف)
p A( ) P A( F) P A( O) P A( J ) P A( E )
p(A F p F| ). ( ) p A O p O( | ). ( ) p A J p J( | ). ( ) p A E p E( | ). ( )
0 5/ 0 25/ 0 7/ 0 25/ 0 8/ 0 2/ 0 3/ 0 3/ 0 55/
P O A( | ) P A O P O( P A| ( )) ( ) / / / 0 32/ (ب
مثال19: سه ماشین C,B,A به ترتیب 60 درصد، 30 درصد و 10 درصد کل محصولات کارخانهای را تولید میکنند درصد محصولات معیوب این ماشینها به ترتیب برابر 2 درصد، 3 درصد، 4 درصد است از میان محصولات این کارخانه محصولی به صورت تصادفی انتخاب میکنیم میخواهیم هر یک از این احتمالات را محاسبه کنیم :
الف : احتمال اینکه معیوب باشد.
ب : احتمال اینکه با ماشین C تولید شده باشد در صورتیکه بدانیم معیوب است.
حل : احتمال معیوب بودن : X
P A( ) 0 6/ , P B( ) 0 3/ , P C( ) 0 1/ P X( | A) 0 02/ , P X( | B ) 0 03/ , P X C( | ) 0 04/ : الف
P(X) P(A)P(X / A) P( B) P(X / B) P(C) P(X /C) ./600/020/030/03 0/100/040/025 : ب
P C P X C( ) ( | )
P C X( | )
P A P X A P B P X B P C P X C( ) ( | ) ( ) ( | ) ( ) ( | )
0 16/
هدف این فصل آشناسازی دانشجویان با متغیرهای تصادفی گسسته، توابع احتمال و توزیعهای مربوط به آنهاست.
متغیر تصادفی گسسته، تابع احتمال و تابع توزیع
متغیر تصادفی گسسته
متغیر تصادفی: تابعی است که روی فضای نمونه تعریف میشود و هر یک از مقادیر آن، متناظر با یک یا چند عضو از اعضای فضای نمونه است. با توجه به این که هر تابع دارای دامنه و حوزه میباشد دامنه یک متغیر تصادفی نیز فضای نمونه ( S ) و حوزهاش مجموعه اعداد حقیقی است.
مثال1: فرض کنید که X قانونی باشد که اگر سکهای پرتاب شود و شیر بیاید، X را برابر یک تعریف کنیم و اگر خط بیاید X را برابر صفر تعریف کنیم.
X :{H T, }{1 0, } X :S
انواع متغیر تصادفی
1- متغیر تصادفی گسسته ؛ با تعداد مقادیر متناهی یا شمارش پذیر
2- متغـیر تصادفی پیوسـته ؛ با تعداد مقادیر ممـکن نامتناهی و غیر قابل شمارش
متغیرهای تصادفی را با حروف بزرگ لاتین مثل Z و Y و X و هر یک از مقادیر انتخابی آنها را با حروف کوچک z و y و x نشان میدهند
تابع احتمال
به تابعی که بتوان با استفاده از آن احتمال هر یک از مقادیر ممکن متغیر تصادفی را مشخص کرد » تابع احتمال « یا » توزیع احتمال « گویند. تابع احتمال تابعی است که دامنه آن مقادیر ممکن متغیر تصادفی و حوزه آن احتمالات مربوط به هر مقدار از متغیر تصادفی است.
در حالت گسسته احتمالها بوسیلهی تابعی به نام تابع احتمال معرفی میشوند که با نماد (p(X x نشان داده میشود. بنابر اصول موضوع احتمال، (p(X x وقتی یک تابع احتمال است که :
x X در حوزه P X( x ) P X( x ) 0 -١
x P X( x ) 1 -2
مثال2: تعداد فروش کت و شلوار فروشگاه لباسی در هر روز، همراه با احتمال آن، در جدول زیر ارائه شده است. آیا میتوان گفت احتمالهای ارائه شده یک تابع احتمال است ؟
X x 1 2 3 4 5 6 7 8
p(X x ) 0/1 0/15 0/16 0/20 0/19 0/08 0/07 0/05
حل :
1)داریم:
P XP X(( 15))0 10 19/ ,/ ,P XP X(( 2)6)0 15/ ,0 08/ ,p XP X(( 3)7)0 16/0 07/ , ,P XP X(( 4)8)0 20/0 05/ ( P X( x ) 0, x ) پس اصل اول برقرار است
(2
1x P X( x ) 1 0 1/ 0 15/ 0 16/ 0 20/ 0 19/ 0 08/ 0 07/ 0 05/ بنابراین، اصول موضوع برقرار است و پاسخ مثبت است.
تابع توزیع ( تابع احتمال تجمعی )
تابع توزیع، تابعی است که به ازای جمیع مقادیر ممکن متغیر تصادفی X، احتمال وقوع مقداری کوچکتر یا مساوی با X را نشان میدهد. یعنی
F x( ) P X( x )
مثال3: در مورد مثال 2 تابع توزیع را محاسبه کنید.
حل:
F( )1 P X( 1) 0 1/ F( )2 P X( 2) P X( 1) P X( 2) 0 1/ 0 15/ 0 25/ F( )3 P X( 3) P X( 1) P X( 2) P X( 3) 0 1/ 0 15/ 0 16/ 0 41/
X x 1 2 3 4 5 6 7 8
p(X x ) 0/1 0/25 0/41 0/61 0/80 0/88 0/95 1/0
امید ریاضی و واریانس متغیر تصادفی
امید ریاضی
امید ریاضی متغیر تصادفی X که با (E (X نشان داده میشود همان میانگین موزون است که احتمالات در آن، نقش ضرایب ( وزنها ) را ایفاء میکنند.
امید ریاضی یک متغیر تصادفی از حاصل جمع ضرب هر متغیر تصادفی در مقدار احتمال خودش بدست میآید. که عبارت فوق را میتوان به صورت زیر بیان کرد.
E X( ) X f X ( )
در عبارت فوق f ( )x همان (P X( x است.
امید ریاضی را میانگین X نیز مینامیم و با x یا نیز نشان میدهیم.
ویژگیهای امید ریاضی
E b( ) b E aX( ) aE X( )
E aX( b) aE X( )b
مثال4: برای مشاهدات مثال2، امید ریاضی X را محاسبه کنید.
4E X( ) 1 0 1/ 2 0 15/ 3 0 16/ 4 0 2/ 5 0 19/ 6 0 08/ 7 0 07/ 8 0 05/ و این مقدار به این معنی است که فروشگاه انتظار دارد به طور متوسط 4 کت وشلوار در روز به فروش برساند.
واریانس متغیر تصادفی X
واریانس را با نماد V(X) نشان داده و میزان پراکندگی را حول میانگین ( امید ریاضی ) نشان میدهد. برای محاسبه واریانس میتوان از دو فرمول زیر استفاده کرد.
1V X ( ) (X )2f X( ) 2 V X ( ) E X( 2) 2
.است f ( )x P X( x ) و E X( ) که
مانند قبل از جذر واریانس انحراف معیار محاسبه میشود. یعنی ( )SD X( ) V X مثال5: برای مشاهدات مثال2 واریانس و انحراف معیار را محاسبه کنید.
V X( ) (X )2 f X( )
(14)2 0 1/ (2 4)2 0 15/ (3 4)2 0 16/ (4 4)2 0 20/
(5 4)2 0 19/ (6 4)2 0 08/ (7 4)2 0 07/ (8 4)2 0 05/
3 6/ V X( ) E X( 2 )2 19 6/ 16 3 6/ E X( 2 ) 12 0 1/ 22 0 15/ 32 0 16/ 42 0 20/
52 0 19/ 62 0 08/ 72 0 07/ 82 0 05/ 19 6/
SD X( ) V X( ) 3 6/ 1 83/
ویژگیهای واریانس
1) V b( ) 0
2) V aX( ) aV X2 ( )
3) V aX( b) aV X2 ( )
تابع احتمال توأم
تابع احتمال توأم عبارتست از فهرستی از زوجهای (X i ,Y j ) و احتمالهای متناظر با آنها، یعنی
.f (X Yi , j ) P X( i x Yi , j y j )
موارد استفاده تابع احتمال توأم
هر گاه پژوهشگر بخواهد رفتار متغیری مثل X را در ارتباط با رفتار متغیر دیگری مثل Y بررسی نماید، از این تابع استفاده میکند.
مثال 6: دو فروشگاه لوازم خانگی را در نظر بگیرید فرض کنید X تعداد یخچالهای فریز فروخته شده در فروشگاه الف و Y تعداد یخچالهای فروخته شدة فروشگاه ب است نمودار زیر نشان دهندة احتمال توام در فروشگاه در هفتة گذشته است که تابع احتمال توام آنها در جدول زیر آمده است.
P( X 1) (الف P(X Y) (ب
P(Y 0 , X 1) (ج Z X Y د) توزیع احتمال
الف) P ( X 1) P(X 1 , Y 0) P( X 1 ,Y 1)0/220/ 350/ 57
ب) P(X Y )P( X 1, Y 0) P(X 2 ,Y 0) P( X 2,Y 1)0/220/150/050/42
ج) P(Y 0 , X 1) P(Y 0 , X 1) P(Y 1 , X 1)0/220/ 350/ 57 ) د
Z X Y 0 1 2 3
f (z) 0/05 0/40 0/50 0/05
احتمالات حاشیه ای
1- احتمالات حاشیهای X : برای پیدا کردن تابع احتمال متغیر تصادفی X
2- احتمالات حاشیهای Y : برای پیدا کردن تابع احتمال متغیر تصادفی Y
با در دست داشتن تابع احتمال توام میتوان احتمال جداگانه هر متغیرتصادفی را پیدا کرد. در مثال قبل تابع احتمال متغیرتصادفی X را میتوان از جمع کردن احتمالات هر سطر و نوشتن آن در حاشیة سمت راست جدول بدست آورد و تابع احتمال متغیرتصادفی Y را از جمع احتمالات هر ستون و نوشتن آنها در حاشیة پائین جدول بدست آورد به این احتمالات »احتمالات حاشیه ای« میگوئیم.
مثال 7: با توجه به جدول احتمال توأم مثال قبل احتمالات حاشیهای را بنویسید و تابع احتمال X و Y را در دو جدول مجزا بنویسید.
حل :
X 0 1 2
f (X) 0/23 0/57 0/20
Y 0 1
f (Y) 0/42 0/58
کوواریانس و استقلال دو متغیر تصادفی
کواریانس
معیار عددی است که نوع و شدت رابطه خطی بین دو متغیر تصادفی را نشان میدهد و عبارتست از امید ریاضی تغییرات دو متغیر بر حسب میانگین شان.
برای محاسبه کوواریانس میتوان از دو فرمول زیر استفاده کرد.
12 COV X YCOV X Y(( ,, ))E XE XY(( )XE X E Y)((Y ) (Y ))
E (XY ) i j x y f x yi j ( i j ) y و x در صورت گسسته بودن
مقادیر مختلف کواریانس
1- کوواریانس مثبت : نشان دهندة رابطة مستقیم دو متغیر است یعنی با افزای ش یکی دیگری نیز افزایش مییابد.
2- کوواریانس منفی : که نشان دهندة رابطة معکوس دو متغیر است یعنی با افزای ش یکی دیگری کاهش مییابد.
3- کوواریانس صفر : که بازگو گنندة استقلال دو متغیر است یعنی هیچ کدام بر یکدیگر تأثیری ندارند.
مثال 8: در مثال 6 کواریانس بین فروش دو فروشگاه را محاسبه کنید. در مورد نوع رابطة دو متغیربحث کنید.
حل:
E(X)x x f (x)00/2310/5720/200/97
E (Y)y yf (y)00/4210/580/58
E XY( )x y f xi j ( i ,y j ) ( 0 0 0 05/ )
i j
(0 1 0 18/ ) (1 0 0 22/ ) ( 1 1 0 35/ ) ( 2 0 0 15/ )
(2 1 0 05/ ) 0 35/ 0 1/ 0 45/
Cov( X ,Y) E (X Y) E (X) E (Y)0/45(0/970/58) 0/1126
Cov XY( ) E X( x )(Y y )
((100 970 97// ))((000 580 58// ))0 220 05// ((100 970 97// ))((110 580 58// ))0 350 18//
/0 1126(2 0 97/ )(00 58/ )0 15/ (2 0 97/ )(10 58/ )0 05/ با توجه به منفی بودن مقدار کوواریانس رابطه بین دو متغیر تصادفی X و Y رابطه معکوس است.
استقلال دو متغیر تصادفی
دو متغیر تصادفی X و Y در صورتی مستقلاند که به ازای تمام زوجهای (X i ,Y j ) رابطه روبرو برقرار باشد. (f (x i , y j ) f (x i )f (y j مثال 9: استقلال دو متغیر X و Y در مثال 6 را بررسی کنید.
f (x y1, 1 ) p X( 0,Y 0) 0 05/ P x( 0)P Y( 0) 0 23/ 0 42/ .بنابراین دو متغیر مستقل نیستند
رابطه استقلال و کواریانس دو متغیر
اگر x و y مستقل باشند، کواریانشان حتماً صفر است ولی عکس قضیه همیشه صادق نیست. به این معنی که اگر کواریانس بین دو متغیر صفر باشد دو متغیر لزوما مستقل نیستند.
معرفی چند توزیع گسسته
توزیع برنولی
ویژگیهای پیشامدهایی که دارای نوزیع برنولی هستند عبارت است :
1- آزمایش فقط یک بار صورت میگیرد.
2- فقط دو پیامد ممکن دارد. (موفقیت و شکست)
3- احتمال موفقیت و شکست ثابت است. ( البته در صورت تکرار آزمایش )
4- آزمایشها مستقل از یکدیگر انجام میشوند.
متغیر مورد نظر: موفقیت یا شکست در آزمایش انجام شده.
مفاهیم p و q درتوزیع برنولی
- P یعنی احتمال موفقیت ( احتمال وقوع پیشامد مورد نظر )
- q یعنی احتمال شکست ( احتمال عدم وقوع پیشامد مورد نظر )
p و q مکمل یکدیگر هستند یعنی p q 1 q 1 p
سوال: آیا پیشامد استخراج شده از نمونه گیری بدون جایگزاری دارای توزیع برنولی است یا خیر؟
پاسخ: نمونه گیریهای بدون جایگزینی از جامعه باعث میشود احتمال موفقیت و شکست در آزمایشها تغییر کرده و شرط سوم از ویژگیهای برنولی نقض گردد و توزیع را از حالت برنولی خارج شود. البته لازم به ذکر است نمونه گیری بدون جایگزینی از جوامع خیلی بزرگ، میتواند به برنولی بودن توزیع کمک نماید. (مثال: در بانکی 5000 نفر دارای حساب بانکی هستند که 2000 نفر آنها دارای حساب کوتاه مدت هستند. اگر موفقیت را داشتن حساب کوتاه مدت تعریف کنیم. پیشامد انتخاب یک نفر از این 5000 نفر دارای توزیع برنولی است. چرا که تمام ویژگیهای توزیع برنولی را داشته و در مورد شرط سوم میتوان گفت احتمال موفقیت فرد اول و احتمال موفقیت فرا دوم همانطور که ملاحظه میشود این دو احتمال تفاوت چندانی با هم ندارند. پس شرط سوم نیز برقرار است.)
پس به طور کلی میتوان گفت نمونه گیری با جایگزینی از کلیه جوامع آماری و نمونه گیری بدون جایگزینی صرفاً از جوامع خیلی بزرگ، میتواند به برنولی بودن توزیع کمک نماید.
میانگین و واریانس توزیع برنولی
x E X( ) p
x2 V X( ) pq
مثال10: اگر در ریختن یک تاس سالم آمدن عدد 4 یا 6 را موفقیت بنامیم و بقیه حالتها را شکست به حساب آوریم، میانگین و واریانس توزیع را حساب کنید. حل : ابتدا ویژگیهای توزیع برنولی را در مورد آن بررسی میکنیم.
1- آزمایش فقط یک بار صورت میگیرد.☺
2- فقط دو پیامد ممکن دارد. (موفقیت و شکست) ☺
3- احتمال موفقیت و شکست ثابت است. ( البته در صورت تکرار آزمایش ) ☺
4- آزمایشها مستقل از یکدیگر انجام میشوند. ☺ بنابراین آزمایش انجام شده دارای توزیع برنولی بوده که احتمال موفقیت و شکست برابر است با
p P X( 1) P T( 4or T 6) 61 61 31
q P X( 0) 1 p
E X( ) p 1
x2 ( ) 3 1 2 2 در نتیجه
V X pq
3 3 9
توزیع دو جمله ای
ویژگیها:
1- تکرار آزمایش ( n بار )
2- هر آزمایشی فقط دو پیامد دارد
3- ثابت بودن p و q در هر آزمایش
4- مستقل بودن آزمایشها از همدیگر متغیر مورد نظر:تعداد موفقیت در n آزمایش انجام شده.
در صورت برقراری شروط فوق آنگاه X تعداد موفقیتها در n تکرار آزمایش دارای توزیع دوجملهای است که با نماد ( , )X ~ binomial n p نشان داده میشود. و فرمول توزیع دو جملهای به صورت زیر بیان میشود.
P X( x ) xn p xq n x
x 0 1 2, , ,...,nاجزاء تشکیل دهنده توزیع دو جمله ای
تعداد آزمایشها = n
تعداد موفقیتهای مورد نظر = x احتمال موفقیت در هر آزمایش = p احتمال شکست در هر آزمایش = q میانگین و واریانس توزیع دو جمله ای
xx2 V XE X(( )) npqnp
n و p و q پارامترهای توزیع دو جملهای هستند.
مثال 11: رستورانی 8 نوع خوراک ماهی، 12 نوع خوراک گوشت و10 نوع خوراک مرغ درست میکند .
اگر مشتریان این رستوران خوراکها را به تصادف انتخاب کنند.
الف) احتمال اینکه دونفر ازچهار مشتری بعدی خوراک ماهی سفارش دهند چقدر است ؟
ب) احتمال اینکه حداکثر دو مشتری از چهار مشتری خوراک ماهی سفارش دهند چقدر است؟ ج) میانگین و واریانس تعداد افرادی که خوراک ماهی سفارش میدهند چقدر است؟
حل: ابتدا توزیع متغیر مورد بررسی را پیدا میکنیم. با توجه به ساختار آزمایش مورد نظر به نظر میرسد متغیر مورد نظر (تعداد مشتریانی که خوراک ماهی سفارش میدهند.) دارای توزیع دوجملهای باشد به همین دلیل شرایط توزیع دو جملهای بررسی میشود.
1- تکرار آزمایش ( n بار ) ☺ (4 مشتری بررسی شده اند.)
2- هر آزمایشی فقط دو پیامد دارد. ☺ (مشتری یا خوراک ماهی سفارش میدهد یا خوراکی غیر ازماهی سفارش میدهد.)
3- ثابت بودن p و q در هر آزمایش ☺ (در صورت مسئله فرض شده مشتریان این رستوران خوراکها را به تصادف انتخاب میکنند. پس p و q ثابت است.)
4- مستقل بودن آزمایشها از همدیگر☺ (نظر هر مشتری مستقل از نظر مشتری دیگر است.) پس متغیر آزمایش X دارای توزیع دو جملهای با پارامترهای 4 و p است.
P X( 2) 42 308 2 2230 4 2 2 4!( 4! 2)! 308 2 2230 2 0 115/ (الف
P X( 2) P X( 0)(X 1) P X( 2)
4 8 0 22 4 0 4 8 1 22 4 1 4 8 2 22 4 2 (ب
0 30 30 1 30 30 2 30 30
وقتی که n نسبتاً بزرگ است، محاسبه احتمال از طریق فرمول کار خسته کنندهای میشود، لذا برای رفع این مشکل از جدولهای مخصوصی استفاده میشود. در این کتاب این جدول در پیوست (1) ارائه شده است. در این جدول احتمال P X( c) xc0 nx p qx n x برای مقادیر مختلف n، p و c آورده شده است. در نتیجه با استفاده از جدول بیان شده و برای 4c 2، n و /0 30p 0 27/ داریم:
P X( 2) 0 916/
E X( ) np 4 308 3230 1 07/ (ج
این مقدار ریاضی بیانگر ان است که انتظار میرود به طور متوسط 07/1 نقر خوراک ماهی سفارش دهند.
V X( ) npq 4 308 2230 0 78/
مقدار p و نوع توزیع
1- اگر 5/0 = p باشد، توزیع متقارن
2- اگر /0 5p باشد، توزیع چوله به چپ
3- و اگر /0 5p باشد، توزیع چوله به راست است
توزیع هندسی
ویژگیها:
1- تکرار آزمایش
2- هر آزمایشی فقط دو پیامد دارد
3- ثابت بودن p و q در هر آزمایش
4- مستقل بودن آزمایشها از همدیگر متغیر مورد نظر: تعداد آزمایش تارسیدن به اولین موفقیت.
در صورت برقراری شروط فوق آنگاه X تعداد آزمایش تارسیدن به اولین موفقیت دارای توزیع هندسی است که با نماد ()X ~Geometric p نشان داده میشود. و فرمول توزیع هندسی به صورت زیر بیان میشود.
P X( x ) q x 1 p , x 1 2 3, , ,...
اجزاء تشکیل دهنده توزیع هندسی تعداد آزمایشهای انجام شده تا رسیدن به اولین موفقیت = x احتمال موفقیت در هر آزمایش = p احتمال شکست در هر آزمایش = q
میانگین و واریانس توزیع هندسی
x E X( ) 1 p
2 ( q
x V X ) p 2
p و q پارامترهای توزیع هندسی هستند.
مثال12: : اگر احتمال قبولی در یک امتحان رانندگی که شخصی هر بار شرکت میکند 75% باشد، احتمال اینکه این شخص سرانجام در چهارمین بار قبول شود، چند است ؟ میانگین و واریانس متغیر مورد نظر را پیدا کنید.
X P X (4 , p 4)0 75/ q x 1 p 0 25/ 4 1 0 75/ 0 012/ :حل
E X( ) 1 1 1 33/ p 0 75/
q
V X( ) p 2 2 0 44/
توزیع دوجملهای منفی
ویژگیها:
1- تکرار آزمایش
2- هر آزمایشی فقط دو پیامد دارد
3- ثابت بودن p و q در هر آزمایش
4- مستقل بودن آزمایشها از همدیگر
متغیر مورد نظر: تعداد آزمایش تارسیدن به k امین موفقیت.
در صورت برقراری شروط فوق آنگاه X تعداد آزمایش تارسیدن به k امین موفقیت دارای توزیع دوجملهای منفی است که با نماد ( , )X ~ NB k p نشان داده میشود. و فرمول توزیع دوجملهای منفی به صورت زیر بیان میشود.
P X( x ) xk 11 p qk x k , x k k, 1,k 2,...
اجزاء تشکیل دهنده توزیع دوجملهای منفی تعداد آزمایشهای انجام شده تا رسیدن بهk امین موفقیت = x احتمال موفقیت در هر آزمایش = p احتمال شکست در هر آزمایش = q
میانگین و واریانس توزیع دوجملهای منفی
k
x E X( ) p
2 ( kq
x V X ) p 2
p و q پارامترهای توزیع دو جملهای منفی هستند.
در صورتی که k برابر 1 باشد توزیع دوجملهای منفی همان توزیع هندسی است.
مثال13: اگر شخصی در معرض ابتلا به یک بیماری مسری قرار داشته باشد، با احتمال 40% به آن دچار میشود. احتمال اینکه 10 امین شخص در معرض بیماری 3 امین شخصی باشد که به آن مبتلا میشود، چقدر است.
حل:
X 10, k 3 , p 0 40/
P X( 10) 103 11 p q3 10 3 360 40/ 3 0 6/ 7 0 064/
k
E X( ) p 7 5/
kq
V X( ) p 2 2 11 25/
مفهوم امید ریاضی در این حالت به این صورت است که انتطار میرود به طور متوسط 5/7 امین نفر سومین نفری باشد که به بیماری مبتلا میشود.
توزیع چند جمله ای
ویژگیها:
1- تکرار آزمایش ( n بار )
2- هر آزمایشی بیش از دو پیامد دارد
3- احتمال هر پیامد در آزمایشهای مختلف ثابت است.( ثابت بودن p1, p2 ,..., pk در هر آزمایش)
4- مستقل بودن آزمایشها از همدیگر
متغیرهای مورد نظر:تعداد هر یک از پیامدها X 1,X 2 ,...,X k در n آزمایش انجام شده.
در صورت برقراری شروط فوق آنگاه تعداد X 1,X 2 ,...,X k در n تکرار آزمایش دارای توزیع چندجملهای است که با نماد ( , )X ~ Multinomial n p نشان داده میشود. و فرمول توزیع چندجملهای به صورت زیر بیان میشود.
P X( 1 x X1, 2 x 2 ,...,X k x k ) x 1 ,x 2n,...,x k p1 x 1 p2 x 2...pk x k
x 1 x 2 ... x k n
اجزاء تشکیل دهنده توزیع چند جملهای تعداد آزمایشها = n
تعداد مورد نظر در هر پیامد: x 1,x 2 ,...,x k احتمال پیامدهای مختلف در هر آزمایش = p1, p2 ,..., pk
مثال 14: رستورانی 8 نوع خوراک ماهی، 12 نوع خوراک گوشت و10 نوع خوراک مرغ درست میکند .
اگر مشتریان این رستوران خوراکها را به تصادف انتخاب کنند.
الف) احتمال اینکه دونفر ازچهار مشتری بعدی خوراک ماهی و یک نفر خوراک گوشت و یک نفر خوراک مرع را سفارش دهند چقدر است ؟
حل: در صورتی که 1X را تعداد افرادی که خوراک ماهی، 2X را تعداد افرادی که خوراک گوشت و 3X را تعداد افرادی که خوراک مرغ سفارش میدهند در نظر بگیریم داریم:
X 1 2,X 2 1,X 3 1 , p1 308 , p2 3012 , p3 3010
P X( 1 2,X 2 1,X 3 1) 42 1 1, , 308 2 3012 1 3010 1 4! 308 2 3012 1 3010 1 0 21/
2 1 1! ! !
توزیع فوق هندسی
ویژگیهای نوزیع فوق هندسی:
حالتی را در نظر میگیریم که از جامعهای با دو حالت ( موفقیت و شکست ) نمونهای تصادفی بدون
جایگذاری داشته باشیم .فرض میکنیم از جامعهای با اندازه N با دو حالت موفقیت ( سالم بودن ) که به تعداد k در جامعه هستند و شکست ( معیوب بودن ) که به تعداد N k در جامعه هستند، داشته باشیم .از این جامعه نمونهای به اندازه n انتخاب میکنیم .فرض میکنیم در این نمونه : X تا از نوع k و بقیه n‐X از نوع N‐k میباشند.
متغیر مورد نظر(X) : تعداد واحدهایی از نمونه که دارای ویژگی مورد نظر هستند. یعنی از k تا مورد نظر انتخاب شده اند.
در صورت برقراری شروط فوق آنگاه X تعداد واحدهای نمونه که دارای ویژگی مورد نظر هستند دارای توزیع فوق هندسی است. و فرمول توزیع فوق هندسی به صورت زیر بیان میشود.
k N k
P X( x ) x Nn x , x 0 1, ,...,k
n
اجزاء تشکیل دهنده توزیع فوق هندسی
تعداد واحدهایی از نمونه که دارای ویژگی مورد نظر هستند = x تعداد واحدهای جامعه که دارای ویژگی مورد نظر هستند.= K تعداد کل جامعه= N
تعداد کل نمونه=n
میانگین و واریانس توزیع فوق هندسی
nk
x E X( ) N
2 ( nk N( 2 (k )(N n)
x V X ) N N 1)
مثال15: فرض میکنیم از جعبهای شامل 6 لامپ که 3 تای آنها سوخته است، 4 لامپ به تصادف و بدون جایگذاری انتخاب میکنیم احتمال اینکه بین این 4 لامپ، 2 لامپ سوخته وجود داشته باشد چقدر است ؟
Nn 4,6,xk 23 nNxk 4 32 2 : حل
3 6 3
p x( 2) 0 6.
4
توزیع پواسون
توزیع پواسون در دو حالت استفاده میشود یکی برای تقریب توزیع دوجملهای و دیگری برای بررسی تعداد مراجعات به سیستم با میانگین در واحد زمان ( t ).
1. توزیع پواسون برای تقریب توزیع دوجمله ای:
ویژگیهای توزیع پواسون برای تقریب توزیع دوجمله ای:
اگر n به سمت بی نهایت و p به سمت صفر میل کند و در عین حال مقدار np ثابت بماند که یا نماد نشان داده میشود (np )، میتوان بجای توزیع دو جملهای از توزیع پواسون استفاده نمود.
متغیر مورد نظر: تعداد موفقیتها در n آزمایش.
در صورت برقراری شروط فوق آنگاه X تعداد موفقیتها در n آزمایش دارای توزیع پواسون است. وفرمول توزیع پواسون به صورت زیر بیان میشود.
e x
P X( x ) x! ,x 0 1 2, , ,...
بعنوان پارامتر توزیع np
e 2 718/
امید ریاضی و واریانس توزیع پواسون
از بین کلیه توزیعهای رایج، توزیع پواسون تنها توزیعی است که میانگین و واریانس آن با هم برابرند. V XE X(( ))
مثال16: احتمال اینکه تیراندازی تیرش به خطا برود 3 درصد است اگر وی 150 تیر شلیک کند هر یک از موارد زیر را محاسبه کنید.
الف) احتمال اینکه 3 تیر به خطا برود.
ب) امید ریاضی و واریانس تعداد تیرهای خطا رفته را محاسبه کنید.
ج) احتمال اینکه حداقل 3 تیر به خطا برود.
جواب :
p 0 03/ , n 150 , np 1500 03/ 4 5/ , X 3
P X( x )e .! x P X( 3)e4 5/ 3(4 5!/ )3 0 1687/ (الف
x
E (X)V(X)np1500/034/5 (ب
وقتی که x نسبتاً بزرگ است، محاسبه احتمال از طریق فرمول کار خسته کنندهای میشود، لذا برایرفع این مشکل از جدولهای مخصوصی استفاده میشود. در این کتاب این جدول در پیوست (2) ارائه شده است. در این جدول احتمال P X( c) xc0 e x! x برای مقادیر مختلف و c آورده شده است.
همینطور با توجه به اینکه فقط برای مقادیر کوچکتر در جدول مقدار ارائه شده است. از قوانین احتمال استفاده کرده و داریم:
P X( x ) 1 P X( x )
P X( x ) 1 P X( x 1)
X-١ ٠x X+١
P a( X b) P X( b) P X( a 1)
ج)
P X( 3) 1 P X( 2) 1 [P X( 0)P X( 1) P X( 2)]
1 (e4 5/ 0(!4 5/ )0 e4 5/ 1!(4 5/ )1 e4 5/ 1!(4 5/ )1 ) 1 0 174/ 0 826/
2- توزیع پواسون برای تعداد مراجعات به سیستم با میانگین در واحد زمان ( t )
ویژگیهای توزیع پواسون تعداد مراجعات به سیستم با میانگین در واحد زمان ( t ): زمانی که تعداد مراجعات به سیستمی با میانگین مراجعه در واحد زمان t انجام میشود مد نظر باشد.
متغیر مورد نظر: تعداد مراجعه.
در صورت برقراری شروط فوق آنگاه X تعداد مراجعات دارای توزیع پواسون است. و فرمول توزیعپواسون به صورت زیر بیان میشود.
e (t) (t)x
P X( x ) x ! ,x 0 1 2, , ,...
که در رابطه فوق متوسط تعداد مراجعات در واحد زمان است و t مدت زمان مراجعات.
مثال17: تعداد اتومبیلهایی که به پمپ بنزینی مراجعه میکند دارای توزیع پواسون با میانگین
5/2 اتومبیل در هر 10 دقیقه میباشد. این احتمالات را محاسبه کنید.
الف) در 10 دقیقه اول بیش از یک اتومبیل مراجعه کند.
ب) در 20 دقیقه بیش از 3 اتومبیل و کمتر یا مساوی 6 اتومبیل مراجعه کند.
ج) در 5 دقیقة اول اتومبیلی مراجعه نکند.
حل:
الف)
در هر 10
2 5/
t 1 t 2 5/ 1 2 5/
P X( 2) 1 P X( 1) 1 0 287/ 0 713/
ب)
t 2 t 2/525
P(3 X 6)P(X 6)P(X 3)0/7620/2650/497
ج)
t 105 21 t2/50/51/25
P X 0 e1/25 0!(1/25)0 0/286
( )
هدف اصلی این فصل آشنا ساختن دانشجویان با متغیرهای تصادفی پیوسته و تعدادی از توابع مهم آنهاست.
احتمال متغیرهای پیوسته
بخاطر این که میزان احتمال در توابع پیوسته در یک نقطه معین مساوی صفر است، لذا در این گونه توابع، احتمال همیشه در قالب یک فاصله تعیین میشود
تابع چگالی احتمال
احتمال این که متغیر تصادفی پیوسته x مقداری بین دو نقطه a و b را بگیرد برابر است با
b
P a( X b) a f X dx( )
که رابطه فوق f(x) تحت عنوان تابع چگالی احتمال شناخته میشود که دارای ویژگیهای زیر است.
1)f x( ) 0 , x
2)f x dx( ) 1
نقش علامت مساوی در احتمالات پیوسته
1) P X( a) aa f x dx( ) 0
2) P a( X b) P a( X b) P a( x b) P a( X b)
پس علامت مساوی در این توزیعها نقشی ایفاء نمیکند.
مثال (1): فرض کنیم تابع چگالی احتمال x به صورت زیر باشد.
f ( )x 0ke3x ,,OWx. 0 . را تعیین کنید k (الف
p( .0 5 x 1) (ب : حل
بنابر ویژگی اول f ( )x همواره باید بزرگتر از صفر باشد بنابراین برای برقرار این شرط 0k باشد.
برای برقراری شرط دوم داریم:
ke3x dx k 0e3x dx 1
k [ 31 e3x ]0 1 k3 [01] k3 1 k 3
f x( ) 3e3x x 0
0 ow
ب)
p( .0 5 x 1) 0 5.1 3e dx3x 30 5.1 e dx3x 3[ 31 e3x ]0 51. 1(e3 e1 5. ) e1 5. e3
تابع توزیع متغیر تصادفی پیوسته
تابع توزیع متغیر تصادفی پیوسته که گاهی تحت عنوان تابع توزیع تجمعی نیز نامیده میشود به صورت زیر تعریف میشود.
FX ( )x p X( x ) x f t dt( )
بدیهی است که 0 (F( و 1 (F( است.
بنا به تعریف تابع توزیع داریم :
( )p(a X b) ab f x dx( ) P X( b)P X( a) F b( )F a مثال(2): در مثال (1)، تابع توزیع را محاسبه کرده و بر اساس آن احتمال (1p( .0 5 x را محاسبه کنید
F xp( .(0 5)xxf t dt1)( ) F ( )10Fx 3( . )e0 53tdt (13(e331)e(3t1)0xe 1 5. )(ee3x1 5.1)e 31 e3x
امید ریاضی متغیر تصادفی پیوسته
یعنی ضرب متغیر تصادفی در تابع چگالی خود و سپس انتگرال گیری به ازای مقادیر ممکن متغیر.
E X( ) X f X dx ( )
واریانس متغیر تصادفی پیوسته
یعنی کسر متغـیر تصادفـی از میانگین خود، به توان 2 رساندن نتیجه و ضرب نتیجه حاصله به تابع چگالی
و انتگرال گیری
X2 V X( ) (x E X( ))2f x dx( )
در محاسبات، واریانس به صورت زیر نیز محاسبه میشود :
X2 E X( 2 ) (E X( ))2 E X( 2 ) 2 x f x dx2. ( ) 2
x
نکته 1 : انحراف معیار : 2
Var ax( b) a2X2 : 2 نکته
مثال (3): فرض میکنیم متغیر تصادفی X دارای تابع چگالی احتمال زیر است :
2 ) , 1 x 1 f ( )x (2x 3x
0 ,OW.
میانگین و واریانس X را محاسبه کنید .
حل :
1
E x( ) x .()(2x 3x dx2 )
1
1 1 (2x 2 3x 3 )dx 1 2
1 2 2 3[ x 3 34 x 4 ]11 32
2 1 1)(2x 3x dx2 ) ( )32
2 E x( 2 )(E x( ))2 x 2.( 2
1
1 ( 1)(2x 3 3x 4 )dx 94 2 21[1 x 4 35 x 5 ]11 94 35 94 6790
1 2
r E X( r ) x f x dxr ( ) ام r نکته: گشتاور مرتبه
تابع چگالی احتمال یکنواخت (مستطیلی)
متغیر تصادفی X دارای تابع چگالی احتمال یکنواخت با پارامترهای و است اگر احتمال وقوع x در فاصلههای هم اندازه در فاصله و برابر باشد. تابع چگالی یکنواخت به صورت زیر تعریف می
شود.
1 , x
f ( )x
0 ,OW.
• ویژگیهای تابع چگالی احتمال یکنواخت
1- نمودار f ( )x برای به صورت زیر است.
2- تابع توزیع ( )F X برابر است با:
0 x
x x
F x( ) P X( x ) f t dt( ) x
1 x
3- دارای میانگین 2 و واریانس 2(12) است.
4- برای 0 1، ، توزیع x را یکنواخت استاندارد گویند.
مثال (4): تابع توزیع متغیر تصادفی x به صورت زیر است.
f (x) 5x15 0 در غیر این
مطلوب است محاسبة :
الف) (10p(0x ب) امید ریاضی و واریانس x حل :
الف) p(0 x10)010101 dx05 101 dx 105 101 dx010x ]105 1
ب) E x( ) 10
v(x) ()2 (155)2
تابع چگالی احتمال نمایی
متغیر تصادفی X دارای تابع چگالی احتمال نمایی با پارامتر است اگر تابع چگالی احتمال آن به صورت زیر باشد.
f ( )x ex ,x 0
0 ,OW.
توزیع نمایی کاربردهای مهمی دارد. به طور مثال اگر تعداد موفقیتها یا ورودیها دارای توزیع پواسون باشد، میتوان نشان داد که زمان انتظار مابین موفقیتها یا ورودیهای متوالی از توزیع نمایی پیروی میکند.
• ویژگیهای توزیع نمایی
1F x( ) P X( x ) x f t dt( ) 1 ex
2 P X( x ) 1 P X( x ) 1 F x( ) ex
3 E X( ) 1 , Var X( ) 12
مثال(5): تعداد اتومبیلهایی که به یک رستوران بین راهی مراجعه میکنند به طور متوسط در هر ساعت 5 اتومبیل میباشد میخواهیم مقادیر زیر را محاسبه کنیم.
الف) به طور متوسط فاصلة زمانی بین مراجعة 2 اتومبیل.
ب) احتمال اینکه فاصلة زمانی بین 2 مراجعه متوالی کمتر از ده دقیقه باشد.
ج) احتمال اینکه 2 مراجعة متوالی بیش از 3 دقیقه طول بکشد.
حل: چون تعداد مراجعات از توزیع پواسون برخوردار است فاصلة زمانی بین دو مراجعه از توزیع نمایی برخوردار است و چون به طور متوسط 5 اتومبیل به رستوران در هر ساعت مراجعه میکنند پس داریم.
515 E(x)1 ب) چون واحد زمانی 10 ساعت است ابتدا ده دقیقه را به ساعت تبدیل میکنیم.
0/167
حال داریم :
565/0P(X0/167)F(0/167)1ex1e5x1e5(0/167) 1e0/833 ج) ابتدا زمان 3 دقیقه را بر حسب ساعت بدست میآوریم.
0/05
P(X 0/05)1 F (0/05) ex e5x e5(0/05) 0/ 779
چند نکته:
1) ab (nx m dx ) n xdxab ab mdx
2)abcdx cx
3)ab xdx 21 x b a
4)ab x dxr r 1 br1 r 1 1ar1
bb 12 b 32 2 a 32
5)a x dx a x dx2 a 3 3
6)ab 1 dx ab x dx21 211 1 x 21 1 ba 2b 21 2a 21 2( b a)
7)abe dx ex x ba eb ea 8)abe dxcx c1 ex ba c1 ea c1 eb
در این فصل دانشجویان با مهمترین و کاربردیترین نوع توزیع از زیر مجموعه توزیعهای پیوسته یعنی توزیع نرمال آشنا میشوند.
تعریف توزیع نرمال
توزیع نرمال توزیعی زنگی شکل است که کاربردهای وسیعی است چرا که اولا خیلی از پدیدههای طبیعی دارای این توزیع هستند و ثانیا شکل حدی بسیاری از توزیعهای دیگر نیز نرمال است.
متغیر تصادفی پیوسته x با میانگین و انحراف معیار ، در صورت داشتن تابع چگالی زیر دارای توزیع
نرمال است
1 21 Xx )2 , x
f ( )x
0 ,ow
در این رابطه ...14159/3 و ...7182/2e است. شکل زیر نشان دهندة منحنی نرمال است.
دو پارامتر توزیع نرمال , است که با مشخص بودن آنها توزیع دقیقاً مشخص و منحنی آن قابل ترسیم
است. بدلیل کاربرد زیاد آن متغیر تصادفی x که دارای توزیع نرمال با میانگین و انحراف معیار است را با (X ~ N (, نشان میدهیم و به این صورت میخوانیم x دارای توزیع نرمال با میانگین و انحراف است.
نقش میانگین در منحنی توزیع نرمال
در یک توزیع نرمال هر قدر میانگین افزایش یابد، باعث میشود که منحنی آن بیشتر به سمت راست انتقال یابد.
شکل زیر دو منحنی نرمال را نشان میدهد که انحراف معیارشان برابر (21) ولی میانگین اولـی کوچکتر از میانگین دومی است (2 1)
X
1 2
نقش انحراف معیار در توزیع نرمال
هر قدر انحراف معیار افزایش یابد، منحنی توزیع نرمال کوتاه تر (بعبارتی پهن تر) میشود.
در ش کل زیر دو منحنی نرمال را نشان م یدهد که میانگ ین شان یکسان (21) ولی انحراف معیار دومی
بزرگتر از انحراف معیار اولی است (21)
2 = X
خصوصیات توزیع نرمال
1- سطح زیر منحنی همیشه برابر یک است.
2- f ( )x همیشه بزرگتر یا مساوی صفر است.
3- حداکثر مقدار تابع در µ = X میباشد.
4- تابع حول میانگین، متقارن است.
5- میانگین و واریانس X به ترتیب µ و 2 میباشد.
6- منحنی در محور Xها، هیچ گاه به صفر نمیرسد.
7- میانگین، میانه و مد با هم برابرند.
8-احتمال x با توجه به انحراف معیارهای مختلف بشرح ذیل است :
1. در صورتی که به اندازه یک انحراف معیار در طرفین میانگین جدا کنیم، سطح حاصله تقریبا برابر 68% سطح خواهد بود .
p(1 X 1 ) 0 68/
2. 4- اگر به اندازهی 2 انحراف معیار در طرفین میانگین جدا کنیم، سطح حاصله تقریبا 95% سطح کل میباشد .
p( 2 X 2 ) 0 95/
3. اگر به اندازهی 3 انحراف معیار جدا کنیم، سطح حاصله تقریبا 7/99% خواهد بود .
p( 3 X 3 ) 0 997/
این مفاهیم در شکل زیر نمایش داده شده است.
3 3 2 2
توزیع نرمال استاندارد
برای این که در حالت کلی هر احتمالی را بتوانیم در توزیع نرمال حساب کنیم، کافی است نرمال را به نرمال استاندارد تبدیل کرده و با استفاده از جدولهای مربوطه مقدار احتمال را محاسبه کنیم.
توزیع نرمال استاندارد، توزیع نرمالی است که دارای میانگین صفر و واریانس 1 است. اگر X متغیری باشد که دارای توزیع نرمال با میانگین و انحراف معیار است یعنی (X ~ N (, . برای تبدیل آن به نرمال استاندارد Z، که دارای توزیع نرمال با میانگین صفر انحراف معیار 1 است به صورت زیر عمل میکنیم.
با کم کردن میانگین از متغیر x و تقسیم نتیجه آن بر انحراف معیار، z بدست میآید
X
z
استفاده از جدول توزیع نرمال استاندارد
بعد از آن که نرمال استاندارد را تعریف کردیم فورا نتیجه میگیریم :
( 2p(x 1 X x 2 ) p(x 1 X x 2) p z( 1 Z z احتمالات ( 2p(z 1 Z z را میتوانیم با استفاده از جدول نرمال استاندارد به راحتی محاسبه کنیم ( استفاده از جدول ) .
جدولهای مورد نظر کتاب مقدار احتمال را از تاعدد بخصوصی میدهد. یعنی ( 1p(Z z • چند نکته در مورد روابط احتمالات در متغیرهای پیوسته اگر Y یک متغیر تصادفی پیوسته باشد.
1) P a Y( b) P a Y( b) P a Y( b) P a Y( b)
2) P Y( a) 1 P Y( a)
3) P a Y( b) P Y( b)P Y( a)
• روشهای استفاده از جدول توزیع نرمال استاندارد
1- استفاده مستقیم : مقدار Z مشخص است و احتمال آن را بدست میآوریم.
مثال 1: مطلوبست محاسبه
p Z( 1 72/ )
P Z( 1 72/ )
P(1 3/ Z 1 75/ )
حل:
P Z( 1 72/ ) 0 9573/ P Z( 1 72/ ) 1 P Z( 1 72/ ) 1 0 9573/ 0 0427/ P(1 3/ Z 1 75/ ) P Z( 1 75/ )P Z( 1 3/ ) 0 9599/ 0 9032/ 0 0567/
مثال2: فرض کنیم X دارای توزیع نرمال با میانگین 35/4 و انحراف معیار 59/0 باشد. مطلوب است احتمال
آن که
P X( 4 35/ ) p X( 5 2/ )
P(2 5/ X 5 5/ )
باشد .
حل: طبق اطلاعات مسئله ( /, /4 35 0 59)X ~ N
برای محاسبه احتمالات فوق ابتدا باید متغیر مورد نظر به نرمال استاندارد تبدیل شود.
P X( 4 35/ ) P( X ) p Z( 0 00/ ) 0 5/
P X( 5 2/ ) P( X 5 2/ 0 59/ 4 35/ ) P Z( 1 44/ ) 1 P Z( 1 44/ ) 1 0 9251/ 0 0749/
P(2 5/ X 5 5/ ) P(2 5/ 0 59/ 4 35/ X 5 5/ 0 59/ 4 35/ )
P( 3 14/ Z 1 95/ ) P Z( 1 95/ )P Z( 3 14/ ) 0 97/ 440 0008/ 0 9736/
مثال3: قطر یک بلبرینگ متغیر نرمال با میانگین 7 سانتیمتر و انحراف معیار 1/0 است. استاندارد فنی قطر این کالا عبارتست از 09/7 X 91/6 و تولید یک بلبرینگ استاندارد 1250 ریال سود دارد. اگر قطر بلبرینگ تولیدی کمتر از 91/6 باشد غیر قابل استفاده است و 1050 ریال زیان دارد و در صورتیکه قطر آن بیش از 09/7 باشد با انجام دادن کار اضافی و صرف هزینهای معادل 200 ریال میتوان آنرا به بلبرینگ استاندارد تبدیل کرد. سود مورد انتظار هر بلبرینگ را حساب کنید.
حل: با توجه به صورت مسأله ما سه حالت داریم که باید احتمال هر یک از این 3 حالت را محاسبه کنیم و بعد از آن در هر کدام از حالتها سودی را که میتوانیم بدست آوریم محاسبه کرده و با ضرب کردن احتمال هر حالت در سود آن، سود مورد انتظار را بدست میآوریم.
احتمال حالت اول) P(6/91 X 7/09)P( Z ) p(0/9Z 0/9)
P(Z 0/9)P(Z 0/9)0/8/590/1841 0/6318
احتمال حالت دوم) P( X 6/91) P(Z ) P(Z 0/9)0/1841
احتمال حالت سوم) P X( 7 09/ )P Z( 7 09/0 1/ 7)P Z( 0 9/)
1 P Z( 0 9/ ) 1 0 8159/ 0 1841/
حالت سوم حالت دوم حالت اول
10502001250 1050- 1250 سود
790(0/63181250)(0/18411050)(0/18411050)789/75 سود مورد انتظار
2- استفاده معکوس : احتمال Z مشخص است و مقدار آن را بدست میآوریم.
در استفاده مستقیم از توزیع نرمال، ابتدا Z را مشخص و سپس احتمال آن را از جدول پیدا میکردیم، در استفاده معکوس، مقدار Z برای مشخص نیست و تنها احتمال آن مشخص است، احتمال را در جدول پیدا کرده و سپس Z متناظر با آن را مشخص میکنیم.
در روش مستقیم برای حل مسائل، ابتدا متغیر تصادفی X را به Z تبدیل و سپس به جدول مراجعه می
کردیم، ولی در روش معکوس، پس از پیدا کردن Z مقدار X را با استفاده از رابطه زیر پیدا میکنیم.
X
Z X Z
مثال 4: می خواهیم مقدار z را در صورتیکه 0485/0P(Z z) را محاسبه کنیم.
حل : ابتدا عدد 0485/0 را از جدول پیدا میکنیم و سپس مقدار z آنرا بـا توجـه بـه سـطر و سـتون مربوط پیدا میکنیم که برابر 66/1 - است پس :
P(Z 1/66)0/0485
مثال 5: متغیر تصادفی x دارای توزیع نرمال با میانگین 12 و انحراف معیار 3 مـی باشـد بـه ازاء چـه مقداری از x رابطة 8508 /0P(X x) برقرار است؟
حل : با توجه به جدول احتمال 8508/0 برابر با 04/1z می باشد یعنی 8508/0P(Z 1/04) پس
:
Z X x z x 121 04/ 3 15 12/
مثال 6: زمان لازم برای صدور کارت برای هر داوطلب شرکت در آزمونی به طور متوسط 110 ثانیـ ه با انحراف معیار 35 ثانیه است که به صورت توزیع نرمال است. میخواهیم موارد زیر را محاسبه کنیم :
الف) کار 85 درصد از کارتهای صادر شده در چه دامنـهای در دو طـرف م یـانگین زمـان صـدور کارت هر داوطلب قرار میگیرد.
ب) کار 5 درصد از داوطلبانی که بیشترین زمان را به خود اختصاص میدهد، حـداقل چقـدر طـول میکشد.
حل :
X Z1 0 2 Z
هدف ما پیدا کردن دو مقدار 1x2 , x است. بطوریکه: /0 85P x( 1 X x 2 )
پس قسمتهاشور نخورده در دو طرف منحنی مساحتی برابر با 15/085/01 دارد که چون توزیـ ع نرمال میباشد و توزیع نرمال حول میانگین متقارن است پس مساحت هـر قسـمتهاشـور نخـورده برابـر است با 075/0 215/0 حال باید مقادیر z را برای دو طرف پیدا کنیم که احتمال آن 075/0 است یعنی :
P X( x 2 ) 0 075/ P Z( z 2 )0 075/
P ZP Z(( z1 44/2 ) )1 0 925/P Z(zz2 2) 1 44/0 075/ P Z( z 2 ) 0 925/
/1 44P X( x 1 ) 0 075/ P Z( z 1 )0 075/ P Z( 1 44/ )0 075/ z 1 حال با توجه به مقادیر 1z2 , z مقدار 1x2 , x را مییابیم پس داریم :
x 2 x 2 z 2 1101 44 35/ ( )150 4/
z 2
z 1 x 1 x 1 z 1 1101 44 35/ ( )59 6/
پس :
59/6 X 150/4 (ب
چون 5 درصد از داوطلبان بیشترین زمان را به خود اختصاص میدهند پس 95 درصد آنها در زمان عادی کارشان انجام میشود با توجه به شکل هدف ما پیدا کردن مقدار x است.
X /0Z
٠
Px(Zzz)0/95x110P(Z(1/1645/645)35)0/95167 /575
پس با توجه به نتایج کار 5 درصدی از داوطلبان که بیشترین زمان را به خود احتصاص میدهند حداقل
575/167 ثانیه طول میکشد.
تقریب توزیع دو جملهای بوسیله توزیع نرمال
در فصل قبل توضیح داده شد که در توزیع دو جملهای وقتی که n خیلی بزرگ شود و P به سـمت صفر میل کند محاسبة احتمال کار دشواری خواهد بود بنابراین در چنین حالتی ( در توزیع دوجملهای با nبرزگ و p کوچک ) از تقریب توزیع پواسون با پارامتر np استفاده میشود.
در صورتی که n بزرگ باشد و p به صفر یا یک نزدیک نباشد توزیـ ع نرمـال تقریـ ب خـوبی بـرای توزیع دو جملهای خواهد بود که در این صورت پارامترهای م یـانگین و انحـراف مع یـ ار بـه صـورت زیـ ر محاسبه خواهد شد :
np npq
بنا به تجربه اگر np و nq هر دو بزرگتر از 5 باشند تقریب نرمال، تقریب خوبی بـرای توزیـ ع دوجملـهای خواهد بود در مواردی که p به 5/0 نزدیک باشد تقریب نرمال برای nهای کوچک نیز خوب است.
همانطور که میدانید توزیع دوجملهای توزیع گسسته است و توزیع نرمال تـوزیعی پیوسـته اسـت مـثلاً در
توزیع دوجملهای با 10n و 4/0P( X 5)، p مقداری مثبت است ولـی در توزیـع نرمـال (5P(X برابر صفر است بنابراین وقتی تقریب نرمال را برای دوجملهای به کار میبریم باید از »تصـحیح پیوسـتگی « استفاده کنیم. لازم به ذکر این نوع تصحیح در تمام مواردی که یک توزیع گسسته بوسیله یک توزیع پیوسته تقریب زده میشود باید انجام شود. در جدول زیر تصحیحهای پیوستگی مختلف آمده شده است :
احتمال مورد نظر از توزیع گسسته (مثلا دو جملهای یا پواسون) احتمال موردنظر از توزیع نرمال
P(X x)
P(X x)
P(X x)
P)X x)
P(X x)P(X x1)
P(x1 x x2) P(x0/5 X x0/5)
P(X x0/5)
P(X x10/5)P(X x0/5) P(X x0/5)
P(X x10/5)P(X x0/5)
P(x1 0/5 X x2 0/5
مثال7: یک شبکه تلویزیونی ادعا میکند که 70 درصد از کل بینندگان تلویزیون وقت خود را به دیدن برنامه خاصی در شیهای سه شنبه اختصاص میدهند. به فرض درست بودن این ادعا، احتمال آنکه از بین 400 بیننده، حداقل 250 نفر از آنان برنامه را تماشا کرده باشند، چقدر است؟
X ~ Binomial (400 0 7, / )
np 400 0 7/ 280 , npq 4000 7/ 0 3/ 84 9 16/
P X( 250) P X( 249 5/ ) P X 249 59 16// 280 P Z( 3 33/ )
P Z( 3 33/ ) 1 P Z( 3 33/ ) 1 0 0004/ 0 9996/
مثال 8: استادی به تجربه دریافته اسـت کـه 45 درصـد از دانشـجو یان در درس خاصـی نمـرة »ب« میگیرند اگر در ترم جاری 25 نفر این درس را با او گرفته باشند احتمال گـرفتن نمـرة »ب« را بـرای ایـ ن تعداد محاسبه کنید.
الف) حداقل 10 نفر ب) بین 8 تا 20 نفر ج) دقیقاً 10 نفر
حل : چون 5np250/4511/25 و 75 / 13nq250/55 بزرگتر از 5 هستند پس تقریب نرمال میتواند تقریب خوبی برای توزیع دوجملهای باشد حال داریم :
np250/4511/25 npq 250/450/55 2/49
با استفاده از تصحیح پیوستگی داریم :
(الف
P(X 10)P(X 9/5)P(Z )P(Z 0/7)1P(Z 0/7)0/7580
(ب
P(8 X 20)P(7/5 X 20/5) P( Z )P(1/51Z 3/71)
P(Z 3/71)P(Z 1/51)10/06550/9345
(ج
P( X 10)P(9/5 X 10/5)P( Z ) P(0/7 Z 0/3)
P(Z 0/3)P(Z 0/7)0/1401
تقریب پواسون بوسیله نرمال
وقتی که میانگین توزیع پواسون نسبتاً بزرگ (λ≤10 ) میشود، میتوان بجای توزیـع پواسـون از فرمول توزیع نرمـال اسـتفاده کـرد . در ایـ ن صـورت م یـانگین و انحـراف مع یـ ار توزیـ ع نرمـال برابـر
.خواهد بود ,
به دلیل گسسته بودن توزیع پواسون و پیوسته بـودن توز یـ ع نرمـال در هنگـام حـل مسـائل با یـ د از تصحیح پیوستگی همانند تقریب دوجملهای به وسیلة نرمال استفاده کرد.
مثال 9: به طور متوسط در هر دقیقه 5/0 مشتری با توزیع پواسون به قسـمت پرداخـت فروشـگاهی مراجعه میکند احتمال اینکه بیش از 20 مشتری در طی نیم ساعت مراجعه کنند چقدر است.
جواب : میانگین تعداد مشتریها را در 30 دقیقه محاسبه میکنیم :
تقریب پواسون بوسیلة تقریب نرمال 10 15t 30 30 0 5/ 15
15 153/87
P(X 20) P(X 20/5)P(Z ) P(Z 1/42)1P(Z 1/42)10/92220/0778
قضیة حد مرکزی
این قضیه بیانگر این موضوع است که اگر 1n، X n ,..., X2 , X متغیر تصادفی مستقل باشند بـه شـرط اینکه n به اندازة کافی بزرگ باشـد آن گـاه متغیـر تصـادفی YX1X2 ...X n دارای توزیـ ع نرمـال بـا Y in1Xi و Y2 in12Xi خواهد بود که 2Xi , Xi به ترتیب میانگین و وار یـانس متغیـر تصـادفی Xi هستند.
توزیع مجموع حداقل 10 متغیر تصادفی (10n) تقریباً نرمال است در ضمن باید به این نکته توجه کنیم که Xiها میتوانند هر توزیعی داشته باشند.
مثال10: کشتارگاهی 470 گوسفند را بدون وزن کردن آنها یکجا میخرد وزن هر گوسفند به طور متوسط 45 کیلوگرم با انحراف معیار 4 است احتمال اینکه وزن این 470 گوسفند بیش از 22 تن باشد، چقدر است.
حل : برای حل این مسئله میتوان از قضیه حد مرکزی استفاده کرد.
x i 4 2x i 16
n
2y 2x i 470 16 7520 y 86 7/ i 1
n
x i 45 y x i 470 45 21150
i 1
p(Y22000)p(z )p(z 9/8)1p(z9/8)110
آمار و کاربرد آن در مدیریت - دکتر حسین زارع، دکتر محمدحسن صیف، دکتر سعید طالبی
شیولسون، استدلال آماری در علوم رفتاری، ج۲، ص۹۵، ترجمه کیامنش، تهران، جهاد دانشگاهی، ۱۳۸۳.
هومن، حیدرعلی، استنباط آماری در پژوهش رفتاری، ص۱۱۵، تهران، سمت، ۱۳۸۷.
هومن، حیدرعلی، شناخت روش علمی در علوم رفتاری، ص۱۶۵، تهران، سمت، ۱۳۸۶.
دلاور، علی، مبانی نظری و عملی پژوهش در علوم انسانی و اجتماعی، ص۷۶-۸۰، تهران، رشد، ۱۳۸۷.
دلاور، علی، احتمالات و آمار کاربردی در روانشناسی و علوم تربیتی، ص۲۱۰-۲۲۵، تهران، رشد، ۱۳۸۶.
تجزیه و تحلیل آماری
منبع: حبیبی، آرش؛ سرآبادانی، مونا. (۱۴۰۱). آموزش کاربردی SPSS. تهران: نارون.

۱۰ مورد از پرکاربردترین انواع نمودارها
حال ۱۰ مورد از انواع مختلف نمودار را بررسی میکنیم. به طور کلی محبوبترین انواع نمودارها شامل موارد زیر هستند:
نمودارهای ستونی (Column charts)؛ کالم
نمودارهای میلهای (Bar charts)؛
نمودارهای دایرهای (Pie charts)؛
نمودارهای دوناتی (Doughnut charts)؛
نمودارهای خطی (Line charts)؛
نمودارهای مساحت (Area charts)؛
نمودارهای پراکندگی (Scatter charts)؛ اسکاتر
نمودارهای عنکبوتی یا راداری (Spider/ Radar charts)؛
نمودار گِیج یا عقربهای (Gauge charts)؛
نمودارهای مقایسهای (Comparison charts).
۱۰ مورد از انواع نمودارها
یکی از بزرگترین چالشها انتخاب مؤثرترین و مناسبترین نوع از انواع نمودار برای کار مورد نظرتان است. به طور کلی اگر میخواهید مناسبترین نوع از انواع نمودار را انتخاب کنید، باید تعداد کل متغیرها، نقاط داده و بازهی زمانی دادههای خود را در نظر بگیرید.
هر نوع از انواع نمودار مزایای خاص خود را دارد. به عنوان مثال نمودارهای پراکندگی برای نشان دادن روابط بین عوامل یا مفاهیم مختلف سودمند هستند، در حالی که انواع نمودار خطی برای نشان دادن روندها مناسبترند.
مطلب مرتبط: نمودار سیستمی؛ ابزاری قدرتمند برای درک سیستمهای پیچیده
۱. نمودارهای ستونی، از انواع نمودار
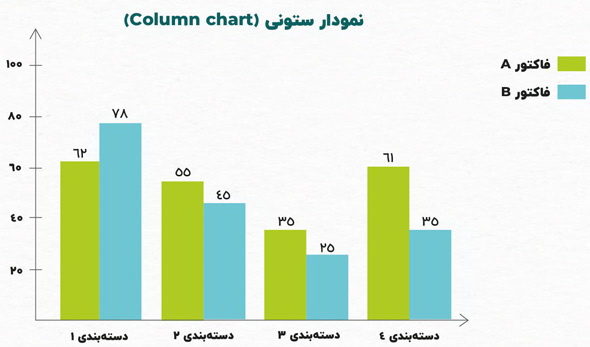
نمودارهای ستونی، از انواع نمودار
نمودارهای ستونی (Column chart) برای مقایسهی حداقل یک مجموعه از نقاط داده مؤثرند. محور عمودی، که به عنوان محور Y نیز شناخته میشود، اغلب برای نشان دادن مقادیر عددی استفاده میشود و محور X در خط افقی یک دوره یا دستههایی را به نمایش میگذارد که مقایسه میشوند.
به طور معمول نقاط داده در نمودارهای ستونی در این انواع هستند: گل، درختچه، خوشهای، انباشته و درختی، که با استفاده از این انواع نقاط داده در رنگهای مختلف میتوانید روندها را پیدا کنید. نمودار ستونی خوشهای به طور ویژه در نمایش و تجزیهوتحلیل چندین مجموعه از دادهها سودمند است. با نمودارهای ستونی انباشته، میتوانید درصد خاصی از دادههای کلی را به سرعت بررسی کنید.
۲. نمودارهای میلهای
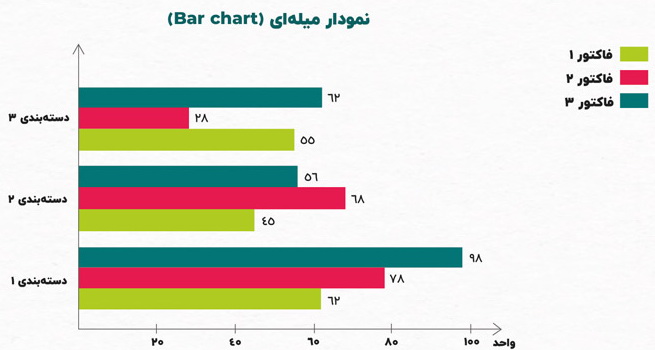
انواع نمودارها - نمودارهای میلهای
نمودارهای میلهای (Bar chart) یک نوع دیگر از انواع نمودار است و برای مقایسهی مفاهیم و درصد در بین عوامل یا مجموعهی دادهها سودمند واقع میشوند. کاربران در این نوع از انواع نمودار میتوانند گزینههای متفاوتی را برای پاسخدهندگان خود تعیین کنند، به عنوان مثال فروش سالانه یا سه ماهه. مشاهده میکنید که نمودارهای میلهای شبیه به نمودارهای ستونی است که در محور X آن قرار دارد.
اگر مطمئن نیستید که چه موقع از نمودارهای میلهای استفاده کنید، باید درمورد نوع خاص دادههای اصلی و ترجیح شخصی خود تصمیم بگیرید. معمولا در مقایسه با انواع دیگر نمودار که در ادامه ذکر میکنیم، نمودارهای میلهای برای نمایش و مقایسهی مجموعههای گستردهی دادهها یا اعداد بهترند.
۳. نمودارهای دایرهای، از انواع نمودار

نمودارهای دایرهای، از انواع نمودار
نمودارهای دایرهای (Pie chart) برای نشان دادن و تفکیک نمونهها در یک بُعد مفیدند. این نمودار به شکل یک دایره است تا رابطهی بین دستههای اصلی و زیر مجموعهی دادههای شما را به نمایش بگذارد. بهتر است هنگام کار با گروههای طبقهبندی شدهی دادهها، یا زمانی که میخواهید تفاوتهایی را بر اساس یک متغیر واحد در بین دادهها نشان دهید، از این نوع از انواع نمودار استفاده کنید.
در واقع شما میتوانید هر گروه دادهی نمونه را در دستههای مختلف، به عنوان مثال جنسیت یا گروههای سنی مختلف، تجزیه کنید. برای پروژههای تجاری میتوانید از نمودارهای نوع دایرهای برای نشان دادن اهمیت یک عامل خاص بر دیگر عوامل بهره ببرید. با این حال برای تجزیهوتحلیل چندین مجموعه دادهی مختلف باید از نمودارهای ستونی کمک بگیرید.
مطلب مرتبط: نمودار ون (Venn): ابزاری برای درک ارتباط بین مجموعهها
۴. نمودارهای دونات یا حلقهای
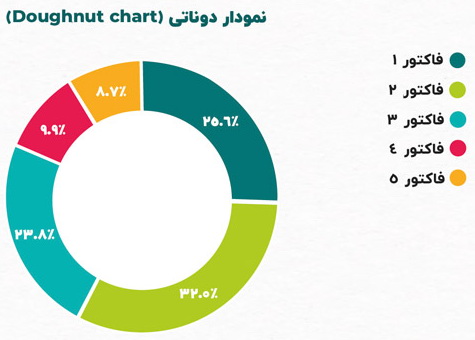
انواع نمودار- نمودارهای دونات یا حلقهای
نمودارهای حلقهای (Doughnut chart) یکی دیگر از انواع نمودار هستند که از نظر مساحت موجود در مرکز برش بسیار به نمودارهای دایرهای شباهت دارند. نمودارهای نوع حلقهای دارای چندین مولفه از جمله تقسیم بخشها و معنای قوس یک بخش جداگانه هستند. این نوع از انواع نمودار برای تبیین رابطه بین نسبت گروههای مختلف داده مناسبند. کاربران در این حالت میتوانند بر نسبت برشها با یکدیگر تمرکز کنند. این نوع از انواع نمودار از طریق فضای خالی میانیشان جزئیات بیشتری را نسبت به نمودارهای دایرهای پوشش میدهند.
۵. نمودارهای خطی
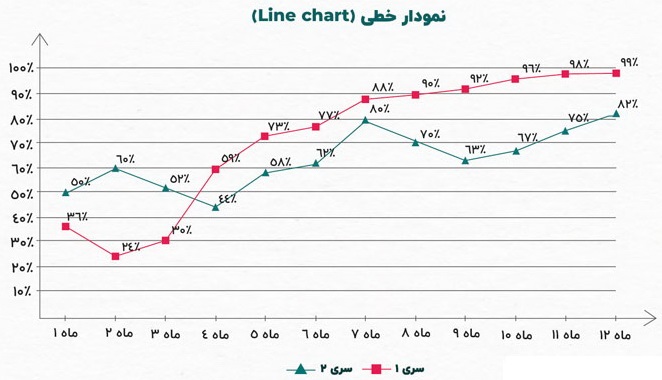
انواع نمودار - نمودارهای خطی
نوع بعدی از انواع نمودار، نمودار خطی (Line chart) است که برای توضیح روند در طی زمان استفاده میشود. محور عمودی همیشه مقدار عددی، و محور X عوامل مرتبط دیگری را نشان میدهد. نمودارهای خطی را میتوان با نشانگرها به شکل حلقه، مربع یا شکلهای دیگر نشان داد.
نمودارهای خطی به اندازهی انواع دیگر نمودارها رنگارنگ نیستند، اما کاربران بهآسانی میتوانند روند مجموعهای از دادهها را در یک دورهی خاص مشاهده کنند. همچنین با این نوع از انواع نمودار میتوانید روند چندین گروه دادهی مختلف را نیز با یکدیگر مقایسه کنید. مدیران یا رهبران مالی ممکن است از نمودارهای خطی برای اندازهگیری و تجزیهوتحلیل روندهای بلند مدت در فروش، دادههای مالی یا آمار بازاریابی استفاده کنند.
مطلب مرتبط: نمودار PERT و کاربرد آن برای برنامهریزی پروژهها (همراه با مثال)
۶. نمودارهای مساحتی، از انواع نمودار
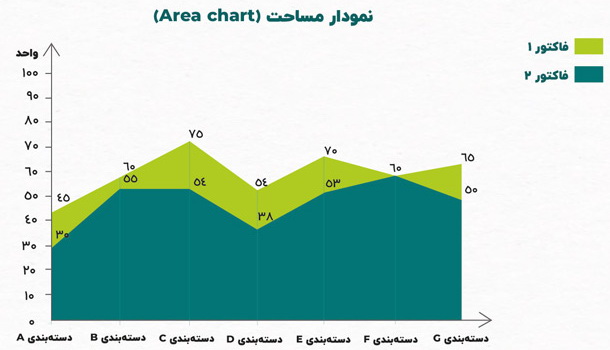
نمودارهای مساحتی، از انواع نمودار
نمودارهای مساحتی (Area chart) که یک نوع دیگر از انواع نمودار هستند، بسیار شبیه به نمودارهای خطیاند، اما مانند موارد قبلی طرحبندی واضحی ندارند. این مورد از انواع نمودار برای نمایش دادن روند در طی یک دوره برای یک یا چند دستهبندی یا تغییرات بین چندین گروه از دادهها ایدئال است. نمودارهای مساحتی دارای دو نوع اصلی هستند: نمودار مساحتی انباشته و نمودار مساحتی تکمیل شده. هر دو نوع میتوانند ماهیت مجموعه دادههای انتخاب شده شما را نشان دهند.
۷. نمودارهای پراکندگی

انواع نمودار - نمودارهای پراکندگی
نوع بعدی از انواع نمودار، نمودارهای پراکندگی (Scatter chart) هستند که برای تحلیل چگونگی قرارگیری اهداف مختلف در اطراف موضوع اصلی و ابعاد مختلف آنها، بیشترین کاربرد را دارد. به عنوان مثال شما میتوانید به سرعت انواع محصولات را بر اساس بودجه و قیمتهای فروش مقایسه کنید. نمودارهای پراکندگی مولفههای مختلفی دارند: نشانگرها، نقاط و خطوط مستقیم. همهی این مولفهها میتوانند واحد دادههای متفاوتی را نشان داده و به هم مرتبط کنند. شما میتوانید نمودار پراکندگی را فقط با نشانگرها یا خطوط ترسیم کنید. به طور کلی نشانگرها برای نقاط دادهی کوچک و خطوط برای نقاط دادهی بزرگ بهتر هستند.
این نوع از انواع مختلف نمودار دارای نقاط مشابهی با نمودارهای خطی هستند، زیرا هر دو از محورهای عمودی و افقی برای نشان دادن نقاط دادهی مختلف استفاده میکنند. اما نمودار پراکندگی همچنین میتواند میزان تفاوت یک متغیر را با دیگری نشان دهند که به عنوان همبستگی شناخته میشود. همبستگیها میتوانند مثبت، منفی یا برابر با صفر باشند. به عنوان مثال میانگین مثبت به این معناست که دادهها در بیشتر اوقات به طور همزمان بر اساس زمان افزایش مییابند.
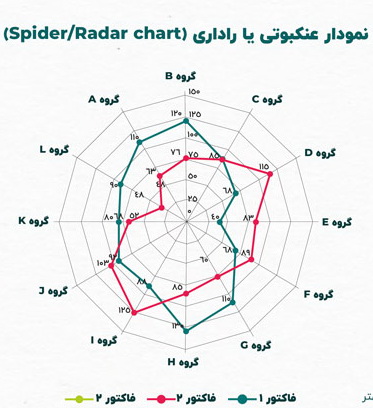
۸. نمودارهای عنکبوتی یا رادار، از انواع نمودار
نمودارهای عنکبوتی یا رادار، از انواع نمودار
نمودارهای عنکبوتی (Spider chart) که یکی دیگر از انواع نموار هستند، به عنوان نمودارهای وب، ستارهای یا نمودارهای قطبی نیز شناخته میشوند. اگر مجموعهی بزرگی از گروههای مختلف داده دارید، استفاده از نمودارهای عنکبوتی بهتر از نمودارهای ستونی به حساب میآید. نمودار رادار در بین انواع نمودار دوبعدی برای نمایش چندین گروه داده برای حداقل سه متغیر در محورها مفید است.
مدیران منابع انسانی معمولا برای بررسی الگوی مهارت گروههای مختلف کارمندان و عملکرد شغلی آنها از این نوع از انواع نمودار استفاده میکنند. علاوه بر این مدیران محصول در آیتی (IT) یا سازمانهای تجاری نیز میتوانند از چنین نمودارهایی برای مقایسهی محصولات مختلف از منظر طیف گستردهای از ویژگیها استفاده کنند، مانند نشان دادن مجموعهای از وسایل برقی مختلف هوشمند بر اساس کیفیت، باتری، ظاهر و پردازندههای آنها به گونهای که مصرفکنندگان بتوانند بهراحتی و بهسرعت بهترین گزینه را بر اساس اولویتهای خود برگزینند. در ادامه به چند مورد دیگر از انواع نمودار میپردازیم.
مطلب مرتبط: نمودار وابستگی چیست و چه کاربردی در حل مشکلات و توسعه فرایندها دارد؟
۹. نمودار گیج یا عقربهای
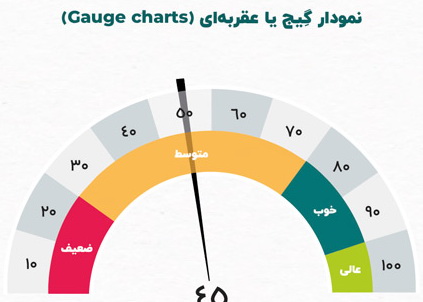
انواع نمودارها - نمودار گیج یا عقربهای
عوامل درنمودار گیج (Gauge) به عنوان مقدارهای مجزا نشان داده میشوند. چنین شاخصهایی معمولا از رنگ قرمز برای پیام اشتباه یا سبز برای موارد صحیح استفاده میکنند. این نوع از انواع نمودار برای نمایش چند شاخص کلیدی عملکرد (KPI)، به ویژه برای برنامههای تجاری، ایدئال هستند. بنابراین این نوع از انواع نمودار معمولا توسط مدیران یا کارفرمایان برای تکالیف جاری استفاده میشود.
مزیت اصلی نمودارهای گیج، نشان دادن میزان پیشرفت در یک هدف است و با نشان دادن عاملی مانند KPI ؛ با ارزیابی تکموردی جزئیات را به گونهای آشکار میکند که درک آن آسان باشد. با این حال یکی از نقاط ضعف این نوع از انواع نمودار محدودیت آن در نشان دادن بیش از یک نقطه داده است. در این حالت نمودار ستونی انتخاب بهتری محسوب میشود.
مطلب مرتبط: شاخصهای کلیدی عملکرد منابع انسانی
۱۰. نمودارهای مقایسهای
انواع نمودار نمودارهای مقایسهای
نمودارهای مقایسهای (Comparison charts)، که به عنوان نمودارهای خوشهای نیز شناخته میشوند، به طور معمول برای مقایسهی حداقل دو شی، واحد یا گروههای داده استفاده میشوند. این نمودار میتواند مقایسهای بصری از جزئیات کیفی و کمی بین دو یا چند چیز ارائه دهد. نمودارهای مقایسهای انواع مختلفی دارند، از جمله مقایسهی بین مؤلفهها، موارد، سریهای زمانی، همبستگیها و توزیع فراوانیها. هدف اصلی نمودارهای مقایسهای نشان دادن نمایی کلی از احتمالات در شرایط مختلف است.
مثالی برای استفاده از نمودارهای مقایسهای
نمودارهای مقایسهای در مباحث تحقیق و فرایند تصمیمگیری برای موضوعات تجاری و علمی نقش پررنگی ایفا میکنند. تصمیمگیرندگان سازمانهای بزرگتر ممکن است برای تجزیهوتحلیل پیشرفت گروههای دادههای مختلف و دادههای رقبا در طی زمان، به مقایسهی جامع و با جزئیات بیشتر نیاز داشته باشند.
مطلب مرتبط: نمودار Swimlane یا خط شنا؛ اهداف، فواید و نحوه رسم این نمودار
نکاتی برای استفاده از انواع نمودارها و چارتها
در این مطلب ۱۰ نوع از بهترین نمودارهای معمول در زندگی روزمره و کاربردهای آنها را بررسی کردیم. در ادامه میتوانید طرحی کلی از مهمترین نکات مربوط به انواع نمودار را مشاهده کنید.
مقادیر داده: شما باید هرگونه جزئیات اضافی مانند رنگ، متن یا خط را از نمودارهای خود حذف کنید. سعی کنید یک نمودار واحد را ساده، یا آن را به دو یا چند نمودار جداگانه تقسیم کنید. متغیرهای موجود در نمودار شما باید مستقیما به واحدهای عددی گروههای دادهی شما متصل شوند؛
ساختار: اطمینان حاصل کنید که نمودارهای شما مقایسههای واضح و آسانی برای خواندن ارائه میدهند. بنابراین باید مجموعه دادههای خود را بر اساس مقادیر منتخب خود به ترتیب واضحی بچینید؛
شاخصها (ایندیکاتور): شاخصها برای برجسته کردن پروژههای شما بسیار مهم هستند. برای جلوگیری از جستوجوی غیرمستقیم، برچسبها را روی خطوط، نوار و بخشهای مناسب خود در نمودارها قرار دهید؛
رنگها و محورها: سعی کنید دستهبندیهای رنگ نمودارهای خود را سادهتر کنید. در دستههای یکسان از همان رنگ در تناژهای متفاوت کمک بگیرید. در نمودارها برای محورها یا برچسبهای یکسان از الگوی رنگی یکسانی استفاده کنید. و اگر نمیتوانید رنگها را در نمودارهای چاپی خود به وضوح ببینید، باید رنگهای موجود را تغییر دهید.
خلاصه
استفاده از نمودار میتواند بررسی اطلاعات و دادههای پیچیده را سادهتر کند. با دیدن یک نمودار به راحتی میتوان به بسیاری از ویژگیهای مجموعهای از اطلاعات و دادهها پی برد. نمودارها اطلاعات عددی و آماری را بهصورت منظم نشان میدهند. در این مطلب انواع نمودار را بررسی کردیم. اگر هنوز هم سؤالی درمورد انواع نمودارها دارید، میتوانید با ما در میان بگذارید.
نمودار خطی
«نمودار خطی» (Line Chart)، دادهها را به عنوان یک سری از نقاط نشان میدهد که به خطوط متصل شدهاند. این نوع نمودار معمولا برای نمایش تغییرات و گرایشها در دادهها مورد استفاده قرار میگیرد.
نمودار ناحیهای
«نمودار ناحیهای» (Area Chart)، بر پایه نمودار خطی است. بنابراین، کارکرد آنها کاملا مشابه است. یک نمودار سطحی، برای نمایش نمایش دادههای کمی به صورت گرافیکی با ترسیم نمودار نقاط داده و اتصال آنها به یکدیگر در بخشهای خطی مورد استفاده قرار میگیرد.
نمودار جعبهای
«نمودار جعبهای» (Box Plot)، معمولا برای تصویر کردن گروهی از دادههای عددی با کمک چارکهای آنها مورد استفاده قرار میگیرد. در نمودار جعبهای، معمولا از برخی شاخصهای پراکندگی برای نمایش تنوع دادههای بیرون از چارکها استفاده میشود.
نمودار بافتنگار
«نمودار بافتنگار» (Histogram) به طور گسترده برای نمایش توزیع دادههای عددی مورد استفاده قرار میگیرد. هر میله در نمودار هیستوگرام یا بافتنگار، نمایشگر دادههای توزیع شده در یک دسته کوچک، یک طیف پیوسته از دادهها و یا تکرار برای نقاط داده خاصی است.
نمودار چگالی
نمودار چگالی (Density Plot) بصریسازی توزیع دادهها در یک دوره پیوسته را انجام میدهد. قلههای نمودار چگالی منعکس کننده تمرکز مقدارها در بازهها است.
علاوه بر آنچه بیان شد، باید متذکر شد که نمودار جعبهای هم در حالتی که متغیرها دارای ترتیب هستند و هم در حالتی که فاقد ترتیب باشند، قابل استفاده است. در ادامه، نگاهی به سمت راست نمودار انداخته میشود. نقطه آغاز مشابه است و این پرسش مطرح میشود که آیا بیش از یک متغیر وجود دارد؟ در صورتی که پاسخ مثبت باشد، به سمت راست نمودار رفته و به پرسشهای دیگر باید پاسخ داد. اگر ویژگیها مشابه نباشند، چه دادهها مرتب شده باشند و چه نباشند، به سمت چپ اینفوگرافیک حرکت میشود. در صورتی که دادهها مرتب نشده باشند، باید از نمودار «نقطهای» (Scatter Plot) استفاده شود. اگر دادهها مرتب شده باشند، باید از نمودار نقطهای یا ناحیهای استفاده شود.
نمودار نقطهای
«نمودار نقطهای» (Scatter Plot یا Scattergram) نوعی از نمودار است که از مختصات دکارتی برای نمایش مقدار دو متغیر متداول برای مجموعه داده استفاده میکند. در این مورد، دادههای ارائه شده به صورت مجموعهای از نقاط ارائه میشوند.
نمودار نقطهای متصل
نمودار نقطهای متصل، بسیار شبیه به نوع قبلی بیان شده در بالا است. تنها تفاوت این دو در آن است که در این نمودار نقاط به یکدیگر متصل شدهاند. در ادامه، نگاهی دقیقتر به مواردی انداخته خواهد شد که در آنها، ویژگیها مشابه هستند. گام بعدی تصمیمگیری پیرامون این است که آیا متغیرها دارای ویژگی سلسله مراتبی هستند؟ اگر پاسخ به این پرسش مثبت است، «نمودار سانکی» (Sankey Diagram) و «نمودار ون» (Venn Diagram) دو گزینه قابل استفاده محسوب میشوند.
نمودار سانکی
نمودار سانکی متعلق به دسته نمودارهای جریان است. این نوع از نمودارها از جهتنماها برای نمایش مقدار جریان به ترتیب، استفاده میکنند.
نمودار وِن
«نمودار ون» (Venn Diagram)، با عناوین دیگری همچون «مجموعه اولیه» (Primary Set) و (نمودار منطقی) (Logical Diagram) نیز نامیده میشود. از این نمودار، برای نمایش همه روابط منطقی موجود بین مجموعه متناهی از چندین مجموعه داده مورد استفاده قرار میگیرد. در این نمودار، عناصر به صورت نقاطی در صفحه و مجموعهها به صورت مناطقی هستند.
اگر هیچ ویژگی سلسله مراتبی در متغیرها وجود نداشته باشد، مسیر روی اینفوگرافیک به سمت چپ رفته و پرسشهایی پیرامون ترتیب دادهها مطرح میشود. اگر متغیرها دارای ترتیب نیستند، گزینههای قابل استفاده «نمودار حرارتی» (Heatmap)، «نمودار درختی» (Treemap)، «نمودار میلهای انباشته» (Stacked Bars) و «نمودار دایرهای» (Pie Chart) خواهند بود. اگر متغیرها دارای ترتیب باشند، «نمودار ناحیه انباشته» (Stacked Area Chart) و «نمودار خطی پشتهای» (Stacked Line Chart) قابل استفاده هستند.
نمودار حرارتی
نمودار حرارتی، یک ارائه گرافیکی از دادهها است که در آن، مقادیر مجزا درون ماتریس با رنگها نمایش داده میشوند. مقادیر بزرگتر، با پیکسلهای تیره و مقادیر کوچکتر با رنگهای روشنتر نمایش داده میشوند.
نمودار درختی
نمودار درختی، دادهها را به شکل مستطیلهایی در سایزهای کوچکتر و بزرگتر نمایش میدهد. اندازه هر مستطیل نشان میدهد که به یک مجموعه تعلق دارد و یا به یک زیر مجموعه.
میلهای انباشته
در صورت استفاده از نمودار میلهای انباشته، بخشی از دادهها تنظیم و یا انباشته میشوند (میلههای افقی، میلههای عمودی یا ستونها) که نشانگر کل میزان دادههای شکسته شده در زیربخشها هستند. بخشهای مساوی در هر نمودار به طور مشابه رنگ میشوند.
نمودار دایرهای
نمودار دایرهای، یک گراف آماری مدور است که بخشها و برشهایی دارد که نشانگر نسبت دادهها هستند. طول کمان در هر بخش، نشانگر مقدار کمی آن بخش است.
انواع متغیرها در تحقیقات علمی و آماری نقشهای مختلفی ایفا میکنند و هر یک ویژگیهای متفاوتی دارند. در ادامه توضیحاتی درباره هر یک از این متغیرها ارائه شده است:
این نوع متغیرها ویژگیهایی از آزمودنیها یا پدیدهها هستند که قابل اندازهگیری و ثبت هستند، اما نمیتوان آنها را در فرآیند تحقیق دستکاری کرد.
این متغیر توسط محقق به صورت آگاهانه دستکاری یا کنترل میشود تا تأثیر آن بر متغیرهای دیگر بررسی شود.
متغیری است که محقق سعی میکند تغییرات آن را به واسطه دستکاری متغیر مستقل مشاهده و اندازهگیری کند. به عبارتی، متغیر وابسته نتیجهای است که تحت تأثیر متغیر مستقل قرار میگیرد.
متغیری است که رابطه بین متغیر مستقل و وابسته را تحت تأثیر قرار میدهد. این متغیر میتواند رابطه بین متغیر مستقل و وابسته را تقویت یا تضعیف کند.
این متغیرها توسط محقق به طور ثابت و کنترلشده نگه داشته میشوند تا تأثیر آنها بر نتیجه کاهش یابد و محقق بتواند تأثیر خالص متغیر مستقل را بررسی کند.
روشهای ناپارامتریک و آمارهای (پارامتریک) هر دو از تکنیکهای آماری هستند، اما تفاوتهای کلیدی بین آنها در فرضیات و نوع دادههایی است که استفاده میکنند.
فرضیات درباره توزیع دادهها: روشهای پارامتریک فرض میکنند که دادهها از یک توزیع خاص پیروی میکنند، معمولاً توزیع نرمال (Gaussian).
نیاز به پارامترها: این روشها نیاز به برآورد پارامترهایی مانند میانگین و واریانس دارند.
کاربرد برای دادههای فاصلهای یا نسبی: روشهای پارامتریک معمولاً برای دادههای فاصلهای (Interval) یا نسبی (Ratio) که در آنها مقادیر معنای عددی دارند، به کار میروند.
مثالها:
مزایا:
معایب:
بدون فرض توزیع خاص: روشهای ناپارامتریک هیچ فرضی درباره توزیع دادهها ندارند و برای دادههایی که توزیع نرمال ندارند یا از نوع رتبهای هستند (Ordinal)، مناسب هستند.
بدون نیاز به برآورد پارامترهای خاص: این روشها به پارامترهای میانگین یا واریانس متکی نیستند.
کاربرد برای دادههای رتبهای یا اسمی: روشهای ناپارامتریک بیشتر برای دادههای رتبهای یا اسمی استفاده میشوند که در آنها فقط ترتیب یا دستهبندی اهمیت دارد، نه مقدار دقیق.
مثالها:
مزایا:
معایب:
دادهها به دو دستهی کلی طبقهبندی نشده و طبقهبندی شده تقسیم میشوند. این دو دستهبندی مربوط به نحوه سازماندهی و نمایش دادهها در تحقیقات آماری و علمی است. در ادامه توضیحی درباره هر یک از این دو نوع داده ارائه شده است:
دادههای طبقهبندی نشده به دادههایی اشاره دارند که به صورت خام و بدون هیچ گونه دستهبندی، سازماندهی یا ترتیب خاصی جمعآوری شدهاند. این دادهها هنوز پردازش نشدهاند و معمولاً به صورت مستقیم از مشاهده، اندازهگیری یا جمعآوری اطلاعات به دست آمدهاند.
ویژگیها:
مثال: نمرات دانشآموزان در یک کلاس به ترتیب ثبت نشده و بدون طبقهبندی: